Page 7 - MODUL MATEMATIKA 9
P. 7
TRANSFORMASI
Perhatikan gambar berikut!
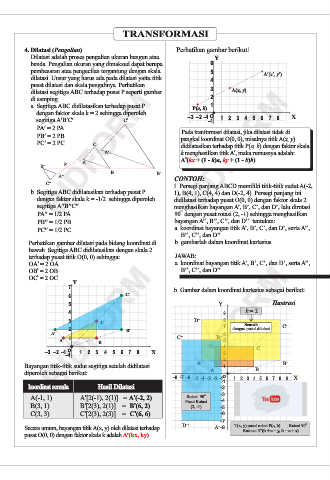
4. Dilatasi (Pengalian) Perhatikan gambar berikut!
Dilatasi adalah proses pengalian ukuran bangun atau Y
benda. Pengalian ukuran yang dimaksud dapat berupa 6
pembesaran atau pengecilan tergantung dengan skala 5
dilatasi. Unsur yang harus ada pada dilatasi yaitu titik A¢(x¢, y¢)
4
pusat dilatasi dan skala pengalinya. Perhatikan
3
BIDFORM
BIDFORM
dilatasi segitiga ABC terhadap pusat P seperti gambar A(x, y)
di samping. 2
a. Segitiga ABC didilatasikan terhadap pusat P 1
dengan faktor skala k = 2 sehingga diperoleh P(a, b)
-3 -2 -1 O 1 2 3 4 5 6 7 8 X
segitiga A¢B¢C¢ C’ -1
PA¢ = 2 PA
Pada tranformasi dilatasi, jika dilatasi tidak di
PB¢ = 2 PB
pangkal koordinat O(0, 0), misalnya titik A(x, y)
PC¢ = 2 PC C
didilatasikan terhadap titik P(a, b) dengan faktor skala
A' k menghasilkan titik A', maka rumusnya adalah:
kx
ky
A A'( + (1 - k)a, + (1 - k)b)
B'' P
B B'
A''
OH:
CONTOH:
CONT
C''
1. Persegi panjang ABCD memiliki titik-titik sudut A(-2,
1. Persegi panjang ABCD memiliki titik-titik sudut A(-2,
b. Segitiga ABC didilatasikan terhadap pusat P 1), B(4, 1), C(4, 4) dan D(-2, 4). Persegi panjang ini
1), B(4, 1), C(4, 4) dan D(-2, 4). Persegi panjang ini
dengan faktor skala k = -1/2 sehingga diperoleh didilatasi terhadap pusat O(0, 0) dengan faktor skala 2
didilatasi terhadap pusat O(0, 0) dengan faktor skala 2
segitiga A¢¢B¢¢C¢¢ menghasilkan bayangan A ’, B’, C’, dan D’, lalu dirotasi
menghasilkan bayangan A’, B’, C’, dan D’, lalu dirotasi
O O
PA¢¢ = 1/2 PA 90 dengan pusat rotasi (2, -1) sehingga menghasilkan
dengan pusat rotasi (2, -1) sehingga menghasilkan
90
bayangan A’’, B’’, C’’, dan D’’. tentukan:
PB¢¢ = 1/2 PB bayangan A ’ ’, B’ ’, C’ ’, dan D’ ’. tentukan:
a. koordinat bayangan titik A’, B’, C’, dan D’, serta A’’,
PC¢¢ = 1/2 PC a. koordinat bayangan titik A ’, B’, C’, dan D’, serta A ’ ’,
’, dan D’
B’’, C’’, dan D’’ ’
B’
’, C’
b. gambarlah dalam koordinat kartesius
Perhatikan gambar dilatasi pada bidang koordinat di b. gambarlah dalam koordinat kartesius
bawah. Segitiga ABC didilatasikan dengan skala 2
AB:
W
JA
terhadap pusat titik O(0, 0) sehingga: JAWAB:
a. koordinat bayangan titik A’, B’, C’, dan D’, serta A’’,
OA' = 2 OA a. koordinat bayangan titik A ’, B’, C’, dan D’, serta A ’ ’,
BIDFORM
BIDFORM
B’’, C’’, dan D’’
OB' = 2 OB B’ ’, C’ ’, dan D’ ’
OC' = 2 OC
Y
7
b. Gambar dalam koordinat kartesius sebagai berikut:
b. Gambar dalam koordinat kartesius sebagai berikut:
6 C¢
5 Y Ilustrasi
4 9 k = 2
3 C D‘ 8
7 Searah C’
2 B¢ dengan pusat dilatasi
A¢ 6
1 C’’ B’’
A B 5
D 4 C
-3 -2 -1 O 1 2 3 4 5 6 7 8 X
-1 3
2
Bayangan titik-titik sudut segitiga setelah didilatasi A’ 1 B‘
diperoleh sebagai berikut: A B
-8 -7 -6 -5 -4 -3 -2 -1 O 1 2 3 4 5 6 7 8 9 X
-1
koordinat semula Hasil Dilatasi -2
-3
O
Rotasi 90
A(-1, 1) A'[2(-1), 2(1)] = A'(-2, 2)
Pusat Rotasi -4
B(3, 1) B'[2(3), 2(1)] = B'(6, 2) (2, -1) -5
C(3, 3) C'[2(3), 2(3)] = C'(6, 6) -6
-7
Secara umum, bayangan titik A(x, y) oleh dilatasi terhadap D’’ A’’ -8 T(x, y) pusat rotasi P(a, b) ...... Rotasi 90 O
Rumus: T’(b + a - y, b - a + x)
pusat O(0, 0) dengan faktor skala k adalah A’(kx, ky)