Page 5 - MODUL MATEMATIKA 9
P. 5
TRANSFORMASI
b. Bayangan titik B(-3, 4) dan C(0, 3) oleh translasi 4. Diketahui segitiga ABC dengan koordinat titik A(-4, 6),
T= (7, -3) adalah B(-5, 3) dan C(-2, 1). Segitiga tersebut ditranslasikan
* B(-3, 4) ® B'(-3 + 7, 4 - 3) ® B'(4, 1) oleh T = (6, -2), dilanjutkan refleksi terhadap garis y = -x
a. Gambarlah segi tiga ABC dan A'B'C’
* C(0, 3) ® C'(0 + 7, 3 - 3) ® C'(7, 0)
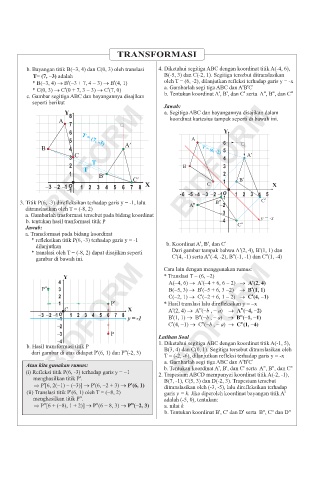
c. Gambar segitiga ABC dan bayangannya disajikan b. Tentukan koordinat A', B', dan C' serta A'', B'', dan C''
seperti berikut
BIDFORM
Jawab:
Y a. Segitiga ABC dan bayangannya disajikan dalam
8
A koordinat kartesius tampak seperti di bawah ini.
7
6 Y
5 T = (7, -3) A 6
A¢
B 4 T = (6, -2) 5
C A'
3 4
T BIDFORM
2 B 3
T
1 B¢ 2
C¢ 1 B’
-3 -2 -1 O 1 2 3 4 5 6 7 8 X C X
-1
-6 -5 -4 -3 -2 -1 O 1 2 3 4 5
-1
3. Titik P(6, -3) direfleksikan terhadap garis y = -1, lalu B'’ C’
A'' -2
ditranslasikan oleh T = (-8, 2)
a. Gambarlah trasformasi tersebut pada bidang koordinat -3 y = -x
b. tentukan hasil tranformasi titik P -4
Jawab: C’’
a. Transformasi pada bidang koordinat
* refleksikan titik P(6, -3) terhadap garis y = -1
dilanjutkan b. Koordinat A', B', dan C’
Dari gambar tampak bahwa A'(2, 4), B'(1, 1) dan
* translasi oleh T = (-8, 2) dapat disajikan seperti
gambar di bawah ini. C'(4, -1) serta A''(-4, -2), B''(-1, -1) dan C''(1, -4)
BIDFORM
BIDFORM
Cara lain dengan menggunakan rumus:
Y * Translasi T = (6, -2)
4 A(-4, 6) ® A'(-4 + 6, 6 - 2) ® A'(2, 4)
P’’ 3 B(-5, 3) ® B'(-5 + 6, 3 -2) ® B'(1, 1)
2 C(-2, 1) ® C'(-2 + 6, 1 - 2) ® C'(4, -1)
1 P’ * Hasil translasi lalu direfleksikan y = -x
C X A'(2, 4) ® A''(-b , - a) ® A''(-4, -2)
-3 -2 -1 O 1 2 3 4 5 6 7 8
-1 y = -1 B'(1, 1) ® B''(-b , - a) ® B''(-1, -1)
-2 C'(4, -1) ® C''(-b , - a) ® C''(1, -4)
-3 P
Latihan Soal
-4 1. Diketahui segitiga ABC dengan koordinat titik A(-1, 5),
b. Hasil transformasi titik P
B(3, 4) dan C(0, 1). Segitiga tersebut ditranslasikan oleh
dari gambar di atas didapat P'(6, 1) dan P''(-2, 3)
T = (-2, -6), dilanjutkan refleksi terhadap garis y = -x
a. Gambarlah segi tiga ABC dan A'B'C’
Atau kita gunakan rumus:
b. Tentukan koordinat A', B', dan C' serta A'', B'', dan C''
(i) Refleksi titik P(6, -3) terhadap garis y = -1 2. Trapesium ABCD mempunyai koordinat titik A(-2, -1),
menghasilkan titik P'.
B(7, -1), C(5, 3) dan D(-2, 3). Trapesium tersebut
Þ P'[6, 2(-1) - (-3)] ® P'(6, -2 + 3) ® P'(6, 1) ditranslasikan oleh (-3, -5), lalu direfleksikan terhadap
(ii) Translasi titik P'(6, 1) oleh T = (-8, 2) garis y = k. Jika diperoleh koordinat bayangan titik A'
menghasilkan titik P''. adalah (-5, 0), tentukan:
Þ P''[6 + (-8), 1 + 2)] ® P''(6 - 8, 3) ® P''(-2, 3) a. nilai k
b. Tentukan koordinat B', C' dan D' serta B'', C'' dan D''