Page 16 - Contoh E-modul utk PKM_Neat

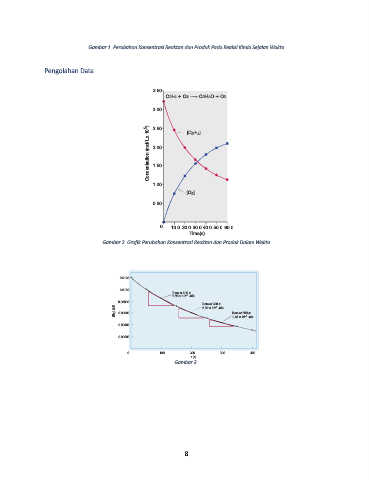
Gambar 1. Perubahan Konsentrasi Reaktan dan Produk Pada Reaksi Kimia Sejalan Waktu

Pengolahan Data
/Volumes/MHDQ-New/MHDQ144/MHDQ144-14
cha75632_ch14_466-509.indd Page 470 9/28/09 2:28:23 PM user-s180 /Volumes/MHDQ-New/MHDQ144/MHDQ144-14
cha75632_ch14_466-509.indd Page 470 9/28/09 2:28:23 PM user-s180
690
Chapter 16 Kinetics: Rates and Mechanisms of Chemical Reactions

3.50 Expressing Rate in Terms of Reactant and Product Concentrations
470 CHAPTER 14 Chemical Kinetics C 2 H 4 # O 3 ±£ C 2 H 4 O # O 2
So far, in our discussion of the reaction of C 2 H 4 and O 3 , we’ve expressed the rate
Figure 14.3 3.00 in terms of the decreasing concentration of O 3 . The rate is the same in terms of
The decrease in bromine concen- C 2 H 4 , but it is exactly the opposite in terms of the products because their con-
tration as time elapses shows up
as a loss of color (from left to centrations are increasing. From the balanced equation, we see that one molecule
right). 2.50 [C 2 H 4 ] of C 2 H 4 O and one of O 2 appear for every molecule of C 2 H 4 and of O 3 that dis-
Concentration (mol/L x 10 5 ) 2.00 Again, note the negative values for the reactants and the positive values for the
appear. We can express the rate in terms of any of the four substances involved:
¢[O 3 ]
¢[C 2 H 4 ]
¢[C 2 H 4 O]
¢[O 2 ]
!"
!#
Rate !"
!#
¢t
¢t
¢t
¢t
1.50
products (usually written without the plus sign). Figure 16.6 shows a plot of the
simultaneous monitoring of one reactant and one product. Because, in this case,
fades (Figure 14.3). Thus, the change in concentration (which is evident by the inten-
1.00
product concentration increases at the same rate that reactant concentration
sity of the color) with time can be followed with a spectrometer (Figure 14.4). We
[O 2 ] plotting the concentration of bromine
can determine the reaction rate graphically by decreases, the curves have the same shapes but are inverted.
versus time, as Figure 14.5 shows. The rate of the reaction at a particular instant is
In many other cases, though, the reactants disappear and the products appear
given by the slope of the tangent (which is D[Br 2 ]yDt) at that instant. In a certain
0.50
25

experiment, we !nd that the rate is 2.96 3 10 M/s at 100 s after the start of the
at different rates. Consider the reaction between hydrogen and iodine to form
25
reaction, 2.09 3 10 M/s at 200 s, and so on. Because generally the rate is propor-
hydrogen iodide:
tional to the concentration of the reactant, it is not surprising that its value falls as
the concentration of bromine decreases. H 2 (g) # I 2 (g)±£ 2HI(g)
30.0 is
If one of the products 0 or reactants 20.0 reaction 40.0 a gas, 60.0 use a manom-
50.0 we can
10.0 of a
8n
For every molecule of H 2 that disappears, one molecule of I 2 disappears and two
eter to !nd the reaction rate. To illustrate this method, let us consider the decomposi-

Time(s)
tion of hydrogen peroxide: molecules of HI appear. In other words, the rate of [H 2 ]decrease is the same as
Gambar 2. Grafik Perubahan Konsentrasi Reaktan dan Produk Dalam Waktu
Figure 16.6 Plots of [C 2 H 4 ]and [O 2 ]
the rate of [I 2 ] decrease, but both are only half the rate of [HI] increase. By refer-
2H 2 O 2 (l) ¡ 2H 2 O(l) 1 O 2 (g)
vs. time. Measuring reactant concentra- ring the change in [I 2 ]and [HI] to the change in [H 2 ], we have
In this case, the rate of decomposition can be conveniently determined by measur-
tion, [C 2 H 4 ], and product concentration,
1 ¢[HI]
[O 2 ], gives curves of identical shapes but
ing the rate of oxygen evolution with a manometer (Figure 14.6). The oxygen Rate !" ¢[H 2 ] !" ¢[I 2 ] !
2H 2 O 2 ¡ 2H 2 O 1 O 2 changing in opposite directions. The ¢t ¢t 2 ¢t
steep upward (positive) slope of [O 2 ]early
0.0120 If we refer the change in [H 2 ] and [I 2 ]to the change in [HI] instead, we obtain
in the reaction mirrors the steep down-
ward (negative) slope of [C 2 H 4 ]because ¢[HI] ¢[H 2 ] ¢[I 2 ]
0.0100 Rate at 100 s: Rate ! !"2 !"2
the faster C 2 H 4 is used up, the faster O 2 ¢t ¢t ¢t
–5
2.96 × 10 M/s
is formed.
0.00800 Notice that this expression is just a rearrangement of the previous one; also note
t 1 [Br 2 ] (M) Rate at 200 s: that it gives a numerical value for the rate that is double the previous value. Thus,
–5
2.09 × 10 M/s
Absorption t 2 t 3 0.00600 Rate at 300 s:
1.48 × 10 M/s
the mathematical expression for the rate of a particular reaction and the numeri-
–5
0.00400 cal value of the rate depend on which substance serves as the reference.
300 400 500 600 We can summarize these results for any reaction,
Wavelength (nm) 0.00200
Figure 14.4 aA # bB ±£ cC # dD
Plot of absorption of bromine
versus wavelength. The maxi- where a, b, c, and d are coefficients of the balanced equation. In general, the rate
mum absorption of visible light 0 100 200 300 400
by bromine occurs at 393 nm. As t (s) is related to reactant or product concentrations as follows:
the reaction progresses (t 1 to t 3 ), Figure 14.5 Gambar 3.
the absorption, which is propor- The instantaneous rates of the reaction between molecular bromine and formic acid at t = 100 s,
tional to [Br 2 ], decreases. 200 s, and 300 s are given by the slopes of the tangents at these times. 1 ¢[A] 1 ¢[B] 1 ¢[C] 1 ¢[D]
Rate !" !" ! ! (16.2)
a ¢t
d ¢t
c ¢t
b ¢t

SAMPLE PROBLEM 16.1 Expressing Rate in Terms of Changes
in Concentration with Time
PROBLEM Because it has a nonpolluting combustion product (water vapor), hydrogen gas
is used for fuel aboard the space shuttles and in earthbound cars with prototype engines:
2H 2 (g) # O 2 (g) ±£ 2H 2 O(g)
(a) Express the rate in terms of changes in [H 2 ], [O 2 ], and [H 2 O] with time.
(b) When [O 2 ]is decreasing at 0.23 mol/L s, at what rate is [H 2 O] increasing?
!
8 PLAN (a) Of the three substances in the equation, let’s choose O 2 as the reference because
its coefficient is 1. For every molecule of O 2 that disappears, two molecules of H 2 dis-
appear, so the rate of [O 2 ]decrease is one-half the rate of [H 2 ]decrease. By similar rea-
soning, we see that the rate of [O 2 ]decrease is one-half the rate of [H 2 O] increase.
(b) Because [O 2 ] is decreasing, the change in its concentration must be negative. We sub-
stitute the negative value into the expression and solve for $[H 2 O]/$t.