Page 16 - Servo Motors and Industrial Control Theory

8 1 Feedback Control Theory

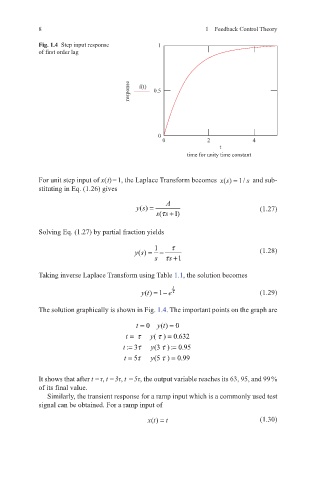
Fig. 1.4 Step input response 1
of first order lag

response f(t) 0.5

0
0 2 4
t
time for unity time constant

For unit step input of x( t) = 1, the Laplace Transform becomes xs() = 1 s / and sub-
stituting in Eq. (1.26) gives
A
() =
ys (1.27)
( ss τ + 1)
Solving Eq. (1.27) by partial fraction yields

1 τ
() =
ys − (1.28)
s τ + 1
s
Taking inverse Laplace Transform using Table 1.1, the solution becomes
t
y () 1t =− e τ (1.29)

The solution graphically is shown in Fig. 1.4. The important points on the graph are

t = 0 y ()t = 0
( ) =
t = τ y τ 0.632
=
t : 3 y τ= τ (3 ) : 0.95
τ
t = 5 y (5 ) = 0.99
τ
It shows that after t = τ, t = 3τ, t = 5τ, the output variable reaches its 63, 95, and 99 %
of its final value.
Similarly, the transient response for a ramp input which is a commonly used test
signal can be obtained. For a ramp input of

xt() = t (1.30)