Page 104 - Microeconomics, Fourth Edition

c03consumerpreferencesandtheconceptofutility.qxd 7/15/10 8:58 AM Page 78

78 CHAPTER 3 CONSUMER PREFERENCES AND THE CONCEPT OF UTILITY

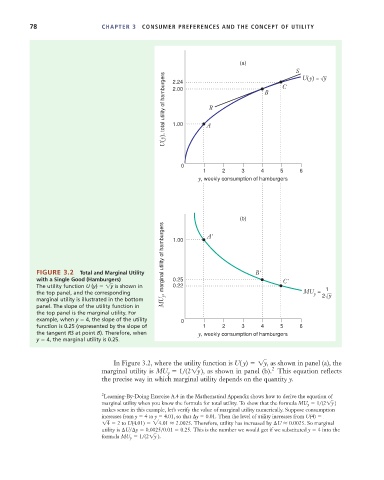
(a)
S U(y) = √y
U(y), total utility of hamburgers 1.00 A R B
2.24
C
2.00

0
1 2 3 4 5 6
y, weekly consumption of hamburgers

(b)
MU y , marginal utility of hamburgers
A'
1.00

FIGURE 3.2 Total and Marginal Utility B'
with a Single Good (Hamburgers) 0.25 C'
The utility function U (y) 1y is shown in 0.22 1
the top panel, and the corresponding MU = 2 √ y
y
marginal utility is illustrated in the bottom
panel. The slope of the utility function in
the top panel is the marginal utility. For
example, when y 4, the slope of the utility 0
function is 0.25 (represented by the slope of 1 2 3 4 5 6
the tangent RS at point B). Therefore, when y, weekly consumption of hamburgers
y 4, the marginal utility is 0.25.

In Figure 3.2, where the utility function is U( y) 1y, as shown in panel (a), the
2
marginal utility is MU 1 (21y ), as shown in panel (b). This equation reflects
y
the precise way in which marginal utility depends on the quantity y.
2 Learning-By-Doing Exercise A.4 in the Mathematical Appendix shows how to derive the equation of
marginal utility when you know the formula for total utility. To show that the formula MU y 1 (21y )
makes sense in this example, let’s verify the value of marginal utility numerically. Suppose consumption
increases from y 4 to y 4.01, so that y 0.01. Then the level of utility increases from U(4)
14 2 to U(4.01) 24.01 L 2.0025. Therefore, utility has increased by ¢U L 0.0025. So marginal
utility is ¢U ¢y 0.0025 0.01 0.25. This is the number we would get if we substituted y 4 into the
formula MU y 1 (21y ).