Page 112 - Basic College Mathematics with Early Integers

SE CT I O N 1. 9 I EXPONENTS, SQUARE ROOTS, AND ORDER OF OPERATIONS 89

#
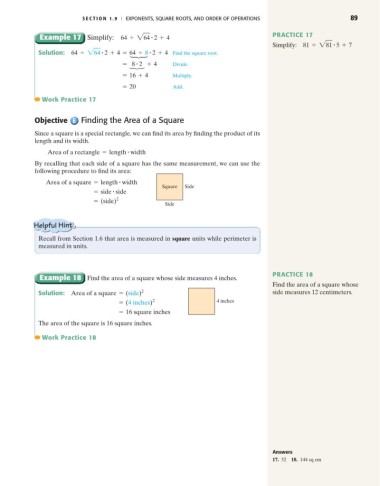
Example 17 Simplify: 64 , 264 2 + 4 PRACTICE 17
#
Simplify: 81 , 281 5 + 7
#
#
Solution: 64 , 264 2 + 4 = 64 , 8 2 + 4 Find the square root.
3
#
= 8 2 + 4 Divide.
3
= 16 + 4 Multiply.
= 20 Add.
Work Practice 17

Objective Finding the Area of a Square
Since a square is a special rectangle, we can find its area by finding the product of its
length and its width.
#
Area of a rectangle = length width
By recalling that each side of a square has the same measurement, we can use the
following procedure to find its area:
#
Area of a square = length width
Square Side
#
= side side
= (side) 2
Side

Recall from Section 1.6 that area is measured in square units while perimeter is
measured in units.

PRACTICE 18
Example 18 Find the area of a square whose side measures 4 inches.
Find the area of a square whose
Solution: Area of a square = (side) 2 side measures 12 centimeters.
= (4 inches) 2 4 inches
= 16 square inches
The area of the square is 16 square inches.

Work Practice 18

Answers
17. 52 18. 144 sq cm