Page 275 - Basic Electrical Engineering

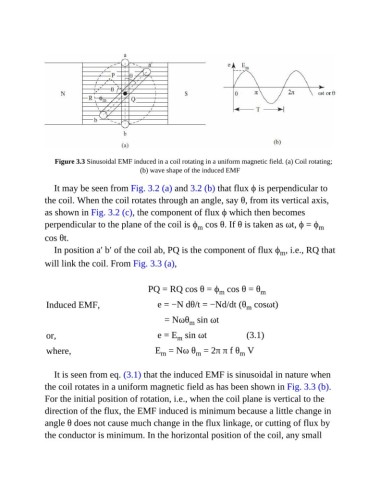
Figure 3.3 Sinusoidal EMF induced in a coil rotating in a uniform magnetic field. (a) Coil rotating;
(b) wave shape of the induced EMF

It may be seen from Fig. 3.2 (a) and 3.2 (b) that flux ϕ is perpendicular to

the coil. When the coil rotates through an angle, say θ, from its vertical axis,
as shown in Fig. 3.2 (c), the component of flux ϕ which then becomes
perpendicular to the plane of the coil is ϕ cos θ. If θ is taken as ωt, ϕ = ϕ m
m
cos θt.

In position a′ b′ of the coil ab, PQ is the component of flux ϕ , i.e., RQ that
m
will link the coil. From Fig. 3.3 (a),

PQ = RQ cos θ = ϕ cos θ = θ m
m
Induced EMF, e = −N dθ/t = −Nd/dt (θ cosωt)
m
= Nωθ sin ωt
m
or, e = E sin ωt (3.1)
m
where, E = Nω θ = 2π π f θ V
m
m
m
It is seen from eq. (3.1) that the induced EMF is sinusoidal in nature when
the coil rotates in a uniform magnetic field as has been shown in Fig. 3.3 (b).

For the initial position of rotation, i.e., when the coil plane is vertical to the
direction of the flux, the EMF induced is minimum because a little change in

angle θ does not cause much change in the flux linkage, or cutting of flux by
the conductor is minimum. In the horizontal position of the coil, any small