Page 107 - E-BOOK MATEMATIKA KELAS XII IPA

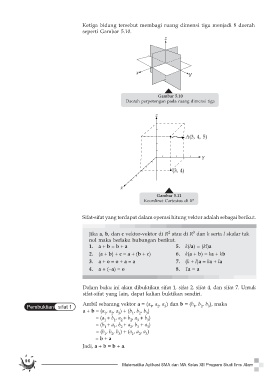
Ketiga bidang tersebut membagi ruang dimensi tiga menjadi 8 daerah
seperti Gambar 5.10.
z

x y

Gambar 5.10
Daerah perpotongan pada ruang dimensi tiga

z

A(3, 4, 5)

y

(3, 4)

x
Gambar 5.11
Koordinat Cartesius di R 3

Sifat-sifat yang terdapat dalam operasi hitung vektor adalah sebagai berikut.

3
2
Jika a, b, dan c vektor-vektor di R atau di R dan k serta l skalar tak
nol maka berlaku hubungan berikut.
1. a b b a 5. k(la) (kl)a
2. (a b) c a (b c) 6. k(a b) ka kb
3. a o o a a 7. (k l)a ka la
4. a (a) o 8. 1a a

Dalam buku ini akan dibuktikan sifat 1, sifat 2, sifat 4, dan sifat 7. Untuk
sifat-sifat yang lain, dapat kalian buktikan sendiri.

Ambil sebarang vektor a (a , a , a ) dan b (b , b , b ), maka
Pembuktian sifat 1 1 2 3 1 2 3
a b (a , a , a ) (b , b , b )
1 2 3 1 2 3
(a b , a b , a b )
1 1 2 2 3 3
(b a , b a , b a )
1 1 2 2 3 3
(b , b , b ) (a , a , a )
1 2 3 1 2 3
b a
Jadi, a b b a.

6
96
Matematika Aplikasi SMA dan MA Kelas XII Program Studi Ilmu Alam