Page 274 - MODUL 12 MIPA

2

KEMIRINGAN GARIS SINGGUNG DAN KEMONOTAN FUNGSI
TRIGONOMETRI

A. Rangkuman
❖ Gradien garis singgung di titik ( , ) adalah
1
1
′
= ( ) = lim ( 1 +ℎ)− ( 1 )
1
ℎ→0 ℎ
❖ Persamaan garis singgung kurva = ( ) dititik ( , ) adalah
1
1

′
– = ( – ), dengan = ( ) = [ ] = 1
1
1
1

❖ Garis normal adalah garis yang tegak lurus terhadap garis singgung pada titiksinggung.
1
Persamaannya adalah – = − ( – )
1
1

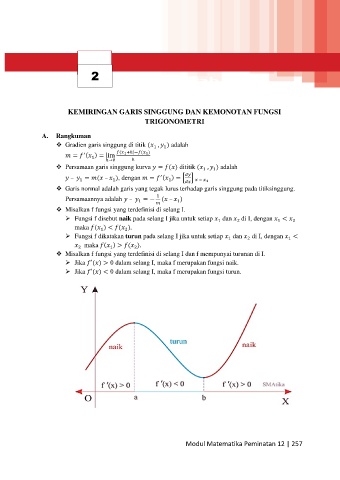
❖ Misalkan f fungsi yang terdefinisi di selang I.
➢ Fungsi f disebut naik pada selang I jika untuk setiap dan di I, dengan <
1
2
1
2
maka ( ) < ( ).
1
2
➢ Fungsi f dikatakan turun pada selang I jika untuk setiap dan di I, dengan <
1
2
1
maka ( ) > ( ).
2
1
2
❖ Misalkan f fungsi yang terdefinisi di selang I dan f mempunyai turunan di I.
➢ Jika ′( ) > 0 dalam selang I, maka f merupakan fungsi naik.
➢ Jika ′( ) < 0 dalam selang I, maka f merupakan fungsi turun.

Modul Matematika Peminatan 12 | 257