Page 186 - NUMINO TG_6A
P. 186
12Increasing at the Same Rate Unit
CMath Vo abulary proportion: an equation that shows to equivalent ratios
Objective: Learn how to write and solve proportions
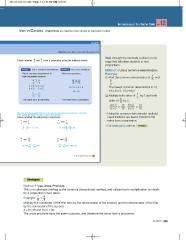
Check whether 4 and 6 form a proportion using the methods below. Walk through the methods outlined on the
6 9 page that will allow students to find
proportions.
Method 1 Use a common denominator. Method 2 Use cross products. Method 1: Use a common denominator.
Find cross products.
Find a common denominator to Example:
write equivalent fractions. 4
Find the common denominator of 6 and
4 =? 6 4 =? 6 6 .
6 9 6 9 9
4 3 =? 6 2 4 9 =? 6 6 The lowest common denominator is 18.
6 3 9 2
18 6 3, 18 9 2
36 = 36
12 12
18 = 18 Multiply both sides of 4 by 3 and both
6
6
The ratios form a proportion. The ratios form a proportion. sides of 9 by 2.
43 12 , 6 2 12
63 18 9 2 18
When the ratios are equivalent fractions or the cross products are the same, they form a proportion. Using the common denominator method,
Have students find whether the pairs of ratios form proportions. equal fractions are found, therefore the
ratios form a proportion.
Check whether the ratios form proportions.
2 and 3 4 and 5
4 6 12 16
6 = 6 12 = 12 , Yes 64 = 60 16 = 15 , No For Method 2, refer to .
12 12 48 48
4 and 8 6 and 15
7 15 8 20
60 = 56 60 = 56 , No 30 = 30 120 = 120 , Yes
105 105 40 40
12. Increasing at the Same Rate 101
Method 2: Use Cross-Products.
This is an alternate method to the common denominator method, and utilizes basic multiplication to check
for a proportion in two ratios.
Example: 4 6
6 9
Multiply the numerator of the first ratio by the denominator of the second, and the denominator of the first
by the numerator of the second.
4 9 36 and 6 6 36.
The cross products have the same outcome, and therefore the ratios form a proportion.
6A Unit 12 169
CMath Vo abulary proportion: an equation that shows to equivalent ratios
Objective: Learn how to write and solve proportions
Check whether 4 and 6 form a proportion using the methods below. Walk through the methods outlined on the
6 9 page that will allow students to find
proportions.
Method 1 Use a common denominator. Method 2 Use cross products. Method 1: Use a common denominator.
Find cross products.
Find a common denominator to Example:
write equivalent fractions. 4
Find the common denominator of 6 and
4 =? 6 4 =? 6 6 .
6 9 6 9 9
4 3 =? 6 2 4 9 =? 6 6 The lowest common denominator is 18.
6 3 9 2
18 6 3, 18 9 2
36 = 36
12 12
18 = 18 Multiply both sides of 4 by 3 and both
6
6
The ratios form a proportion. The ratios form a proportion. sides of 9 by 2.
43 12 , 6 2 12
63 18 9 2 18
When the ratios are equivalent fractions or the cross products are the same, they form a proportion. Using the common denominator method,
Have students find whether the pairs of ratios form proportions. equal fractions are found, therefore the
ratios form a proportion.
Check whether the ratios form proportions.
2 and 3 4 and 5
4 6 12 16
6 = 6 12 = 12 , Yes 64 = 60 16 = 15 , No For Method 2, refer to .
12 12 48 48
4 and 8 6 and 15
7 15 8 20
60 = 56 60 = 56 , No 30 = 30 120 = 120 , Yes
105 105 40 40
12. Increasing at the Same Rate 101
Method 2: Use Cross-Products.
This is an alternate method to the common denominator method, and utilizes basic multiplication to check
for a proportion in two ratios.
Example: 4 6
6 9
Multiply the numerator of the first ratio by the denominator of the second, and the denominator of the first
by the numerator of the second.
4 9 36 and 6 6 36.
The cross products have the same outcome, and therefore the ratios form a proportion.
6A Unit 12 169