Page 209 - NUMINO TG_6A
P. 209
104_G6U13_TG 2014.4.17 6:55 PM ˘ ` 192
Challenge Shadows
jOb ective Learn similarity and proportions to determine the heights of objects by measuring shadow
lengths.
1. Textbook Instructions Challenge Shadows
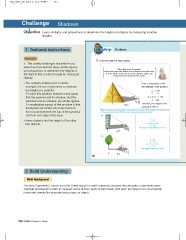
1. This activity challenges students to use 1 . Find the height of each object.
what they have learned about similar figures
and proportions to determine the heights of Place a stick next to the pyramid.
tall objects that could not easily be measured Measure the length of the shadow of the pyramid and the length of the
directly.
stick. The triangle made by the stick and its shadow is similar to the
The sample problem uses a classic triangle made by the pyramid and its shadow.
example, the use of geometry to measure
the height of a pyramid. Form a proportion to find
To solve this problem students must grasp the height(h) of the pyramid.
that the pyramid and its shadow, and the
yardstick and its shadow, are similar figures. h h = 160
A complicating aspect of this problem is that 5 8
the figures are similar only if we measure
from a point beneath the top of the pyramid, 5 ft h 8 = 5 160
not from one edge of the base.
160 ft h = 100
Have students find the height of the other 8 ft
two objects.
Therefore, the height of the
pyramid is 100 ft.
Make sure students understand this concept before moving on. When looking at the picture above,
do they see similar figures? What are the corresponding sides and angles?
a.
h = 42
3 4
3 ft h 4 = 3 42
h = 31.5
The height of the building is 31.5 ft.
4 ft
42 ft
b. h = 60
5 15
118
h 15 = 5 60
5 ft h = 20
The height of the tree is 20 ft.
15 ft
60 ft
2. Build Understanding
The word “geometry” comes from the Greek words for earth measure, because the principles of geometry were
originally developed in order to measure areas of land, such as farm fields, that were too large to be conveniently
measured directly (for example using ropes as rulers).
192 NUMINO Teacher s Guide
Challenge Shadows
jOb ective Learn similarity and proportions to determine the heights of objects by measuring shadow
lengths.
1. Textbook Instructions Challenge Shadows
1. This activity challenges students to use 1 . Find the height of each object.
what they have learned about similar figures
and proportions to determine the heights of Place a stick next to the pyramid.
tall objects that could not easily be measured Measure the length of the shadow of the pyramid and the length of the
directly.
stick. The triangle made by the stick and its shadow is similar to the
The sample problem uses a classic triangle made by the pyramid and its shadow.
example, the use of geometry to measure
the height of a pyramid. Form a proportion to find
To solve this problem students must grasp the height(h) of the pyramid.
that the pyramid and its shadow, and the
yardstick and its shadow, are similar figures. h h = 160
A complicating aspect of this problem is that 5 8
the figures are similar only if we measure
from a point beneath the top of the pyramid, 5 ft h 8 = 5 160
not from one edge of the base.
160 ft h = 100
Have students find the height of the other 8 ft
two objects.
Therefore, the height of the
pyramid is 100 ft.
Make sure students understand this concept before moving on. When looking at the picture above,
do they see similar figures? What are the corresponding sides and angles?
a.
h = 42
3 4
3 ft h 4 = 3 42
h = 31.5
The height of the building is 31.5 ft.
4 ft
42 ft
b. h = 60
5 15
118
h 15 = 5 60
5 ft h = 20
The height of the tree is 20 ft.
15 ft
60 ft
2. Build Understanding
The word “geometry” comes from the Greek words for earth measure, because the principles of geometry were
originally developed in order to measure areas of land, such as farm fields, that were too large to be conveniently
measured directly (for example using ropes as rulers).
192 NUMINO Teacher s Guide