Page 28 - C:\Users\asus\Documents\Chapter 2\

 Teorema 1

Jika R adalah relasi pada A = {a , a ,… a }, maka
2
1
n
M  M e M
Bukti: R 2 R R

Misalkan M = [m ] dan M R2 = [n ]. Menurut definisi, elemen ke-i, ke-j dari M ⊙ M sama
R
ij
R
ij
R
dengan 1 jika hanya jika baris i dari M dan kolom j dari M memiliki 1 pada posisi relatif
R
R
yang sama, katakanlah posisi k. Ini berarti m = 1 dan m = 1 untuk beberapa k, 1 ≤ k ≤ n.
kj
ik
Menurut definisi matriks M , kondisi sebelumnya berarti bahwa a R a , dan a R a. Jadi ai
j
R
k
k
i
R a, dan n = 1. Oleh karena itu, posisi i, j dari M ⊙ M adalah 1 jika dan hanya jika n = 1.
2
ij
j
R
R
ij
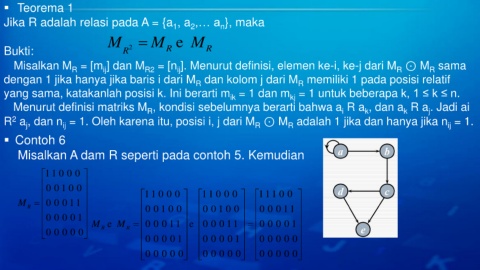
 Contoh 6
Misalkan A dam R seperti pada contoh 5. Kemudian
 1 1 0 0 0 
 
 0 0 1 0 0   1 1 0 0 0   1 1 0 0 0   1 1 1 0 0 

M   0 0 0 1 1       
 R   0 0 1 0 0   0 0 1 0 0   0 0 0 1 1 

 0 0 0 0 1  M e M   0 0 0 1 1  e  0 0 0 1 1    0 0 0 0 1
  0 0 0 0 0   R R      

 0 0 0 0 1   0 0 0 0 1   0 0 0 0 0 
 0 0 0 0 0   0 0 0 0 0   0 0 0 0 0 





