Page 31 - REVISTA 2017

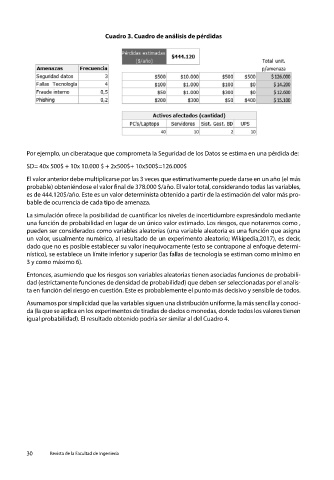
Cuadro 3. Cuadro de análisis de pérdidas

Por ejemplo, un ciberataque que comprometa la Seguridad de los Datos se estima en una pérdida de:
SD= 40x 500$ + 10x 10.000 $ + 2x500$+ 10x500$=126.000$

El valor anterior debe multiplicarse por las 3 veces que estimativamente puede darse en un año (el más
probable) obteniéndose el valor final de 378.000 $/año. El valor total, considerando todas las variables,
es de 444.120$/año. Este es un valor determinista obtenido a partir de la estimación del valor más pro-
bable de ocurrencia de cada tipo de amenaza.

La simulación ofrece la posibilidad de cuantificar los niveles de incertidumbre expresándolo mediante
una función de probabilidad en lugar de un único valor estimado. Los riesgos, que notaremos como ,
pueden ser considerados como variables aleatorias (una variable aleatoria es una función que asigna
un valor, usualmente numérico, al resultado de un experimento aleatorio; Wikipedia,2017), es decir,
dado que no es posible establecer su valor inequívocamente (esto se contrapone al enfoque determi-
nístico), se establece un límite inferior y superior (las fallas de tecnología se estiman como mínimo en
3 y como máximo 6).
Entonces, asumiendo que los riesgos son variables aleatorias tienen asociadas funciones de probabili-
dad (estrictamente funciones de densidad de probabilidad) que deben ser seleccionadas por el analis-
ta en función del riesgo en cuestión. Este es probablemente el punto más decisivo y sensible de todos.
Asumamos por simplicidad que las variables siguen una distribución uniforme, la más sencilla y conoci-
da (la que se aplica en los experimentos de tiradas de dados o monedas, donde todos los valores tienen
igual probabilidad). El resultado obtenido podría ser similar al del Cuadro 4.

30 Revista de la Facultad de Ingeniería