Page 311 - C:\Users\azizu\Documents\Flip PDF Professional\Matematics-Form-1-1\

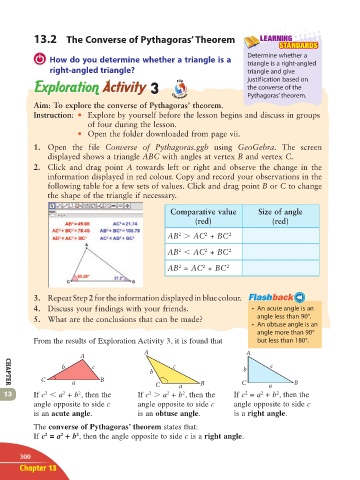
13.2 The Converse of Pythagoras’ Theorem LEARNING
STANDARDS

How do you determine whether a triangle is a Determine whether a
triangle is a right-angled
right-angled triangle? triangle and give
3 Classroom justification based on
Flip
the converse of the
Pythagoras’ theorem.
Aim: To explore the converse of Pythagoras’ theorem.
Instruction: • Explore by yourself before the lesson begins and discuss in groups
of four during the lesson.
• Open the folder downloaded from page vii.
1. Open the file Converse of Pythagoras.ggb using GeoGebra. The screen
displayed shows a triangle ABC with angles at vertex B and vertex C.
2. Click and drag point A towards left or right and observe the change in the
information displayed in red colour. Copy and record your observations in the
following table for a few sets of values. Click and drag point B or C to change
the shape of the triangle if necessary.

Comparative value Size of angle
(red) (red)

AB  AC + BC 2
2
2
AB  AC + BC 2
2
2
AB = AC + BC 2
2
2

3. Repeat Step 2 for the information displayed in blue colour.
4. Discuss your findings with your friends. • An acute angle is an
5. What are the conclusions that can be made? angle less than 90°.
• An obtuse angle is an
angle more than 90°
From the results of Exploration Activity 3, it is found that but less than 180°.
A A
A
b c c b c
b
C a B C a B C a B
CHAPTER
13 If c  a + b , then the If c  a + b , then the If c = a + b , then the
2
2
2
2
2
2
2
2
2
angle opposite to side c angle opposite to side c angle opposite to side c
is an acute angle. is an obtuse angle. is a right angle.
The converse of Pythagoras’ theorem states that:
2
2
2
If c = a + b , then the angle opposite to side c is a right angle.
300
Chapter 13
13 TB Math F1.indd 300 11/10/16 12:22 PM