Page 88 - C:\Users\azizu\Documents\Flip PDF Professional\Matematics-Form-1-1\

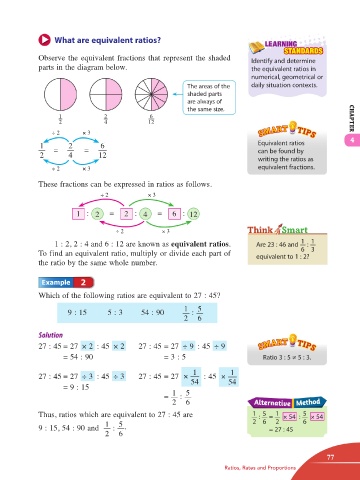
What are equivalent ratios?
LEARNING
STANDARDS
Observe the equivalent fractions that represent the shaded Identify and determine
parts in the diagram below. the equivalent ratios in
numerical, geometrical or
The areas of the daily situation contexts.
shaded parts
are always of
the same size.
1 2 6
2 4 12 CHAPTER
÷ 2 × 3 4
1 = 2 = 6 Equivalent ratios
2 4 12 can be found by
writing the ratios as
÷ 2 × 3 equivalent fractions.
These fractions can be expressed in ratios as follows.
÷ 2 × 3

1 : 2 = 2 : 4 = 6 : 12
Think Smart
÷ 2 × 3
1
1
1 : 2, 2 : 4 and 6 : 12 are known as equivalent ratios. Are 23 : 46 and :
6
To find an equivalent ratio, multiply or divide each part of equivalent to 1 : 2? 3
the ratio by the same whole number.
2

Which of the following ratios are equivalent to 27 : 45?

1 5
9 : 15 5 : 3 54 : 90 :
2 6

27 : 45 = 27 × 2 : 45 × 2 27 : 45 = 27 ÷ 9 : 45 ÷ 9
= 54 : 90 = 3 : 5 Ratio 3 : 5 ≠ 5 : 3.

1 1
27 : 45 = 27 ÷ 3 : 45 ÷ 3 27 : 45 = 27 × : 45 ×
54 54
= 9 : 15
= 1 : 5
2 6
5
5
1
Thus, ratios which are equivalent to 27 : 45 are 1 : = × 54 : × 54
2 6 2 6
1 5
9 : 15, 54 : 90 and : . = 27 : 45
2 6
77
Ratios, Rates and Proportions

04 TB Math F1.indd 77 11/10/16 12:12 PM