Page 228 - Secundaria - Matemáticas 3 - McGraw Hill

EVALUACIÓN
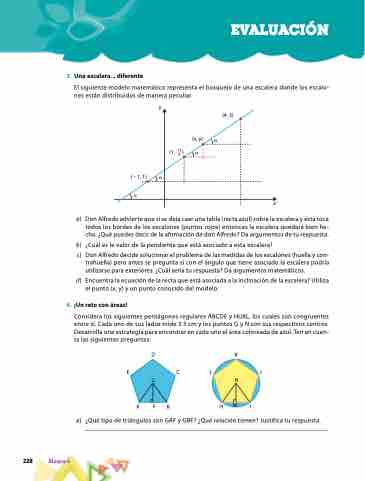
3. Una escalera... diferente
El siguiente modelo matemático representa el bosquejo de una escalera donde los escalo-
nes están distribuidos de manera peculiar.
y
a
(4, 5)
(x, y)
(1, 13 ) 5
a a
(21, 1) a
a) Don Alfredo advierte que si se deja caer una tabla (recta azul) sobre la escalera y ésta toca todos los bordes de los escalones (puntos rojos) entonces la escalera quedará bien he- cha. ¿Qué puedes decir de la afirmación de don Alfredo? Da argumentos de tu respuesta.
b) ¿Cuál es le valor de la pendiente que está asociado a esta escalera?
c) Don Alfredo decide solucionar el problema de las medidas de los escalones (huella y con- trahuella) pero antes se pregunta si con el ángulo que tiene asociado la escalera podría utilizarse para exteriores. ¿Cuál sería tu respuesta? Da argumentos matemáticos.
d) Encuentra la ecuación de la recta que está asociada a la inclinación de la escalera? Utiliza el punto (x, y) y un punto conocido del modelo.
4. ¡Un reto con áreas!
Considera los siguientes pentágonos regulares ABCDE y HIJKL, los cuales son congruentes entre sí. Cada uno de sus lados mide 3.5 cm y los puntos G y N son sus respectivos centros. Desarrolla una estrategia para encontrar en cada uno el área coloreada de azul. Ten en cuen- ta las siguientes preguntas:
DK
ECLJ GN
AFB HMI
a) ¿Qué tipo de triángulos son GAF y GBF? ¿Qué relación tienen? Justifica tu respuesta. ______________________________________________________________________________
x
228 Bloque 4