Page 93 - Buku Teks Digital Mate KSSM T5

Bab 3 Penaakulan Logik

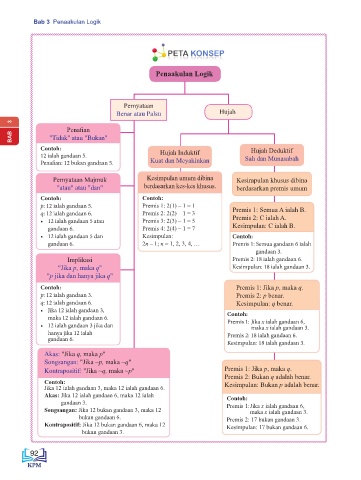
PETA KONSEP

Penaakulan Logik

Pernyataan
Benar atau Palsu Hujah

3
Penafian
BAB "Tidak" atau "Bukan"
Contoh: Hujah Deduktif
12 ialah gandaan 5. Hujah Induktif Sah dan Munasabah
Penafian: 12 bukan gandaan 5. Kuat dan Meyakinkan

Pernyataan Majmuk Kesimpulan umum dibina Kesimpulan khusus dibina
"atau" atau "dan" berdasarkan kes-kes khusus. berdasarkan premis umum
Contoh: Contoh:
p: 12 ialah gandaan 5. Premis 1: 2(1) – 1 = 1
q: 12 ialah gandaan 6. Premis 2: 2(2) – 1 = 3 Premis 1: Semua A ialah B.
• 12 ialah gandaan 5 atau Premis 3: 2(3) – 1 = 5 Premis 2: C ialah A.

gandaan 6. Premis 4: 2(4) – 1 = 7 Kesimpulan: C ialah B.
• 12 ialah gandaan 5 dan Kesimpulan: Contoh:
gandaan 6. 2n – 1; n = 1, 2, 3, 4, … Premis 1: Semua gandaan 6 ialah
gandaan 3.
Implikasi Premis 2: 18 ialah gandaan 6.
"Jika p, maka q" Kesimpulan: 18 ialah gandaan 3.
"p jika dan hanya jika q"
Contoh: Premis 1: Jika p, maka q.
p: 12 ialah gandaan 3. Premis 2: p benar.
q: 12 ialah gandaan 6. Kesimpulan: q benar.
• Jika 12 ialah gandaan 3, Contoh:

maka 12 ialah gandaan 6. Premis 1: Jika x ialah gandaan 6,
• 12 ialah gandaan 3 jika dan maka x ialah gandaan 3.
hanya jika 12 ialah Premis 2: 18 ialah gandaan 6.
gandaan 6.
Kesimpulan: 18 ialah gandaan 3.
Akas: "Jika q, maka p"
Songsangan: "Jika ~p, maka ~q"
Kontrapositif: "Jika ~q, maka ~p" Premis 1: Jika p, maka q.
Premis 2: Bukan q adalah benar.
Contoh: Kesimpulan: Bukan p adalah benar.
Jika 12 ialah gandaan 3, maka 12 ialah gandaan 6.
Akas: Jika 12 ialah gandaan 6, maka 12 ialah Contoh:
gandaan 3. Premis 1: Jika x ialah gandaan 6,
Songsangan: Jika 12 bukan gandaan 3, maka 12 maka x ialah gandaan 3.
bukan gandaan 6. Premis 2: 17 bukan gandaan 3.
Kontrapositif: Jika 12 bukan gandaan 6, maka 12 Kesimpulan: 17 bukan gandaan 6.
Saiz sebenar
bukan gandaan 3.

92