Page 85 - การสำรวจภาพถ่าย Photogrammetry

55
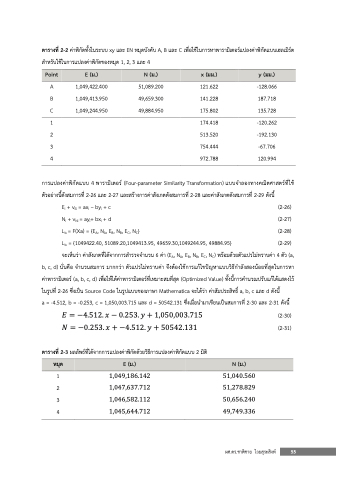
ตารางที่ 2-2 คาพิกัดทั้งในระบบ xy และ EN หมุดบังคับ A, B และ C เพื่อใชในการหาพารามิเตอรแปลงคาพิกัดแบบเฮลเมิรต สําหรับใชในการแปลงคาพิกัดของหมุด 1, 2, 3 และ 4
Point E (ม.) N (ม.) x (มม.)
y (มม.)
A 1,049,422.400
B 1,049,413.950
C 1,049,244.950
1
2 3 4
51,089.200 49,659.300 49,884.950
121.622 -128.066 141.228 187.718 175.802 135.728 174.418 -120.262 513.520 -192.130 754.444 -67.706 972.788 120.994
การแปลงคาพิกัดแบบ 4 พารามิเตอร (Four-parameter Similarity Transformation) แบบจําลองทางคณิตศาสตรที่ใช ตัวอยางนี้ดังสมการที่ 2-26 และ 2-27 และสรางการคาสังเกตดังสมการที่ 2-28 และคาสังเกตดังสมการที่ 2-29 ดังนี้
Ei + vEi = axi – byi + c
Ni + vNi = ayi+ bxi + d
Lb = F(Xa) = {EA, NA, EB, NB, EC, NC}
Lb = {1049422.40, 51089.20,1049413.95, 49659.30,1049244.95, 49884.95}
จะเห็นวา คาสังเกตที่ไดจากการสํารวจจํานวน 6 คา (EA, NA, EB, NB, EC, NC) พรอมดวยตัวแปรไมทราบคา 4 ตัว (a,
b, c, d) นั่นคือ จํานวนสมการ มากกวา ตัวแปรไมทราบคา จึงตองใชการแกไขปญหาแบบวิธีกําลังสองนอยที่สุดในการหา คาพารามิเตอร (a, b, c, d) เพื่อใหไดคาพารามิเตอรที่เหมาะสมที่สุด (Optimized Value) ทั้งนี้การคํานวณปรับแกไดแสดงไว ในรูปที่ 2-26 ซึ่งเปน Source Code ในรูปแบบของภาษา Mathematica จะไดวา คาสัมประสิทธิ์ a, b, c และ d ดังนี้
a = -4.512, b = -0.253, c = 1,050,003.715 และ d = 50542.131 ซึ่งเมื่อนํามาเขียนเปนสมการที่ 2-30 และ 2-31 ดังนี้
= −4.512. − 0.253. + 1,050,003.715 = −0.253. + −4.512. + 50542.131
ตารางที่ 2-3 ผลลัพธที่ไดจากการแปลงคาพิกัดดวยวิธีการแปลงคาพิกัดแบบ 2 มิติ หมุด E (ม.)
1 1,049,186.142
2 1,047,637.712
3 1,046,582.112
4 1,045,644.712
(2-30) (2-31)
(2-26) (2-27) (2-28) (2-29)
N (ม.)
51,040.560 51,278.829 50,656.240 49,749.336
ผศ.ดร.ชาติิชาย ไวยสุุระสุิงห์์
55