Page 53 - MATERI AJAR E-MODUL KALKULUS-1-edit_Neat

2
−1
Jadi lim ( ) ada, meskipun 1 ∉ dan (1)
→1 −1
tidak terdefinisi. Hal ini sah, karena limit fungsi
di suatu titik tidak mensyaratkan nilai fungsi di

titik tersebut harus ada.

Kondisi 3

+ 1, > 1
Diketahui fungsi h yang ditentukan oleh ℎ( ) = { . Jelas bahwa nilai h(1) ada,
2
, ≤ 1
namun apakah lim ℎ( ) ada?. Melalui bantuan tabel, akan ditunjukan limit fungsi h di sekitar
→1
1.

Tabel 7. Nilai pendekatan ℎ( ) untuk mendekati 1 dari kiri

0,6 0,7 0,8 0,9 0,99 0,999 .... 1

ℎ( ) 0,36 0,49 0,64 0,81 0,9801 0,998001 .... 1

Berdasarkan tabel, nampak ℎ( ) ⟶ 1 untuk ⟶ 1 dari kiri, ditulis lim ℎ( ) = 1
−
→1

Tabel 6. Nilai pendekatan ℎ( ) untuk mendekati 1 dari kanan ( x > 1)

1 .... 1,001 1,01 1,1 1,2 1,3 1,4

ℎ( ) 2 .... 2,001 2,01 2,1 2,2 2,3 2,4

Berdasarkan perhitungan numerik, ℎ( ) ⟶ 2 untuk ⟶ 1 dari kanan ditulis lim ℎ( ) =2
+
→1

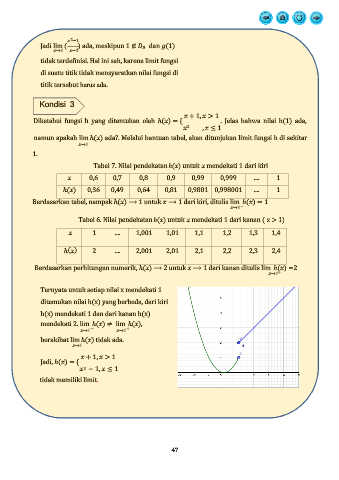
Ternyata untuk setiap nilai x mendekati 1

ditemukan nilai h(x) yang berbeda, dari kiri
h(x) mendekati 1 dan dari kanan h(x)
mendekati 2. lim ℎ( ) ≠ lim ℎ( ),
+
→1 − →1
berakibat lim ℎ( ) tidak ada.
→1

+ 1, > 1
Jadi, ℎ( ) = {
− 1, ≤ 1
2
tidak memiliki limit.

47