Page 210 - Buku Paket Kelas 12 Matematika

Contoh Soal 4.2.1
%XNWL .RQMHNWXU .HVHEDQJXQDQ VHJLWLJD 6XGXW􏰁6XGXW􏰁6XGXW
Misalkan diberikan dua segitiga ABD dan DEF􏰒 GL PDQD 􏰫A dan 􏰫C 􏰫F, PDND ¨ABD ¨DEF 􏰎VHEDQJXQ􏰏􏰃
%XNWL􏰅
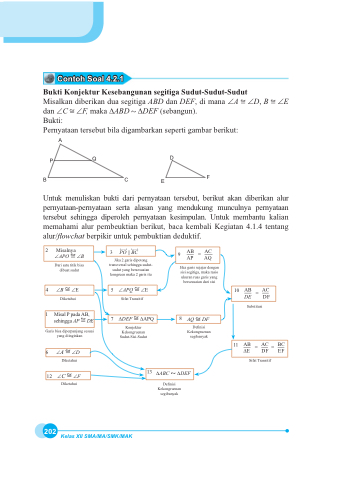
3HUQ\DWDDQ WHUVHEXW ELOD GLJDPEDUNDQ VHSHUWL JDPEDU EHULNXW􏰅
􏰫D􏰒 B 􏰫E
A
P
Q
D
E
BC
F
8QWXN PHQXOLVNDQ EXNWL GDUL SHUQ\DWDDQ WHUVHEXW􏰒 EHULNXW DNDQ GLEHULNDQ DOXU
pernyataan-pernyataan serta alasan yang mendukung munculnya pernyataan tersebut sehingga diperoleh pernyataan kesimpulan. Untuk membantu kalian PHPDKDPL DOXU SHPEHXNWLDQ EHULNXW􏰒 EDFD NHPEDOL .HJLDWDQ 􏰇􏰃􏰂􏰃􏰇 WHQWDQJ alur/ÀRZFKDW EHUSLNLU XQWXN SHPEXNWLDQ GHGXNWLI􏰃
2 Misalnya
􏰫APO 􏰫B
m􏰬o m􏰬o
3 PO || BC
􏰌 $% AC $P AQ
Dari satu titik bisa dibuat sudut
Diketahui
*DULV ELVD GLSHUSDQMDQJ VHVXDL yang diinginkan
Diketahui
12 􏰫C 􏰫F Diketahui
202 Kelas XII SMA/MA/SMK/MAK
Jika garis sejajar dengan VLVL VHJLWLJD􏰒 PDND UDVLR ukuran ruas garis yang bersesuaian dari sisi
8 AQ DF 'H¿QLVL
Kekongruenan segibanyak
Substitusi
6LIDW 7UDQVLWLI
Jika 2 garis dipotong transversal sehingga sudut- sudut yang bersesuaian kongruen maka 2 garis itu
6LIDW 7UDQVLWLI
Konjektur Kekongruenan Sudut-Sisi-Sudut
4 􏰫B 􏰫(
5 􏰫APQ 􏰫(
10$% AC DE DF
􏰂 0LVDO 3 SDGD $%􏰒 sehingga AP DE
􏰊 ¨DEF ¨$34
11 $% AC BC '( DF EF
6 􏰫A 􏰫D
13 ¨ABC ¨DEF
'H¿QLVL Kekongruenan segibanyak