Page 16 - eBook Panduan

LEMBAR KERJA PESERTA DIDIK (LKPD 4)

KOMPETENSI DASAR:
3.4. Menjelaskan keberkaitan turunan pertama dan kedua fungsi dengan nilai maksimum, nilai
minimum, selang kemonotonan fungsi, kemiringan garis singgung serta titik belok dan selang
kecekungan kurva fungsi trigonometri
4.4. Menyelesaikan masalah yang berkaitan dengan nilai maksimum, nilai minimum, selang
kemonotonan fungsi, dan kemiringan garis singgung serta titik belok dan selang kecekungan kurva
fungsi trigonometri

TUJUAN:
Setelah mengikuti proses pembelajaran, peserta didik diharapkan dapat:
1. Memahami keterkaitan turunan fungsi trigonometri dengan kemonotonan grafiknya.
2. Mengidentifikasi dan menentukan titik stationer, dan garis singgung kurva fungsi trigonometri.
3. Menentukan selang kecekungan kurva fungsi trigonometri.
4. Melukis grafik fungsi trigonometri

RINGKASAN MATERI:
A. Interval Fungsi Naik dan Turun/Kemonotonan Fungsi
Syarat sebuah fungsi naik atau turun adalah dengan menggunakan turunan pertama f’(x), yaitu :
1. Fungsi naik apabila f’(x) > 0
2. Fungsi monoton atau stationer apabila f’(x) = 0
3. Fungsi turun apabila f’(x) < 0

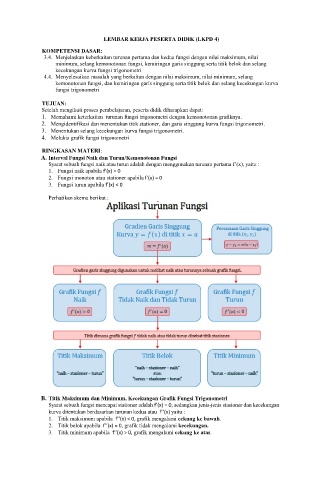
Perhatikan skema berikut :

B. Titik Maksimum dan Minimum, Kecekungan Grafik Fungsi Trigonometri
Syarat sebuah fungsi mencapai stationer adalah f’(x) = 0, sedangkan jenis-jenis stasioner dan kecekungan
kurva ditentukan berdasarkan turunan kedua atau f’’(x) yaitu :
1. Titik maksimum apabila f’’(x) < 0, grafik mengalami cekung ke bawah.
2. Titik belok apabila f’’(x) = 0, grafik tidak mengalami kecekungan.
3. Titik minimum apabila f’’(x) > 0, grafik mengalami cekung ke atas.