Page 77 - analysinew
P. 77
77
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
2. ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ
2
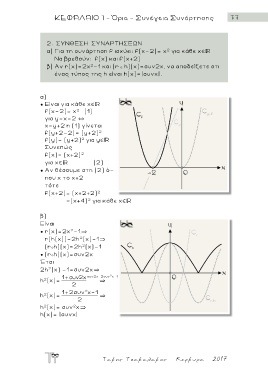
α) Για τη συνάρτηση f ισχύει: f(x-2)= χ για κάθε χ
Nα βρεθούν: f(χ) και f(χ+2)
2
β) Αν r(x)=2x -1 και (r ο h)(x)=συν2χ, να αποδείξετε οτι
ένας τύπος της h είναι h(χ)=|συνχ|.
α )
● Είναι για κάθε χ
f(x-2)= χ (1)
2
για y=x-2 `
x=y+2 η (1) γίνεται
f(y+2-2)= (y+2)
2
f(y)= (y+2) για y
2
Συνεπώς
f(χ)= (χ+2)
2
για χ (2)
● Αν θέσουμε στη (2) ό-
που χ το χ+2
τότε
f(χ+2)= (χ+2+2) 2
=(χ+4) για κάθε χ
2
β )
Είναι
● r(x)=2x -1~
2
r(h(x))=2h (x)-1~
2
(r οh)(x)=2h (x)-1
2
● (r οh)(x)=συν2χ
Έτσι
2h (x) -1=συν2χ~
2
1 2 συν2χ = 2συν χ - 1
2
h (x)= ~
2
2
2
h (x)= 1 2συν χ - 1 ~
2
2
2
2
h (x)= συν x~
h(x)= |συνx|
Τακης Τσακαλακος Κερκυρα 2017