Page 210 - chapter 1

210
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Έστω μια συνάρτηση f που είναι ορισμένη σε ενα σύνολο
της μορφής (α, x 0) (x 0, β). Ορίζουμε
● lim f(x)= + , όταν για κάθε Μ > 0 υπάρχει δ > 0 τέτοιο,
x x 0
ώστε για κάθε χ (α, x 0) (x 0, β), με 0 < | x – x 0 | < δ να
ισχύει: f(x) > M
● lim f(x)=- , όταν για κάθε Μ > 0 υπάρχει δ > 0 τέτοιο,
x
x
0
ώστε για κάθε χ (α, x 0) ( x 0, β), με 0 < | x – x 0 | < δ να
ισχύει: f(x) > - M

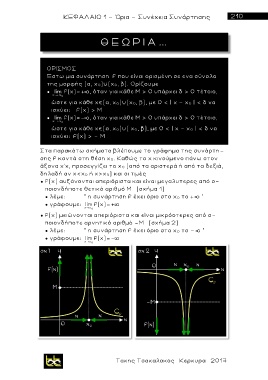
Στα παρακάτω σχήματα βλέπουμε το γράφημα της συνάρτη-

σης f κοντ ά στη θέση χ 0. Καθώς το χ κινούμενο πάνω στον

άξονα χ'χ, προσεγγίζει το x 0 (από τα αριστερά ή από τα δεξιά,
δηλαδή αν χ<x 0 ή χ>x 0) και οι τιμές

● f(x) αυξάνονται απεριόριστα και είναι μεγαλυτερες από ο-

ποιονδήποτε θετικό αριθμό Μ (σχήμα 1)

● λέμ ε : " η συνάρτηση f έχει όριο στο χ 0 το + "

● γ ρ άφ ο υμε: lim f(x)= +
x x 0
● f(x) μειώνονται απεριόριστα και είναι μικρόοτερες από ο-

ποιονδήποτε αρνητικό αριθμό -Μ (σχήμα 2)
● λέμε: " η συνάρτηση f έχει όριο στο χ 0 το - "

● γ ρ άφ ο υμε: lim f(x)=-
x x 0

Τακης Τσακαλακος Κερκυρα 2017