Page 211 - chapter 1

211
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΣΥΝΕΠΕΙΕΣ ΟΡΙΣΜΟ Υ
Με τη βοήθεια του ορισμού α π οδεικνύονται οι παρακάτω
ιδιότητες:
● Αν lim f(x)= , τότε f(x)>0 κοντά στο x 0,
x x 0
ε ν ώ
αν lim f(x) , τότε f(x)<0 κοντά στο x 0
x x 0
● Αν lim f(x)= , τότε lim(-f(x))=- ,
x x 0 x x 0
ε ν ώ

αν lim f(x) , τότε lim(-f(x))=
x x 0 x x 0
1
● Αν lim f(x)= ή , τότε lim = 0
x x 0 x x 0 f(x)
1
● Αν lim f(x)= 0 και f(x)>0 κοντά στο x 0, τότε lim = ,
x x 0 x x 0 f(x)
ε ν ώ

αν lim f(x)= 0 και f(x)<0 κοντά στο x 0, τότε
x x 0
lim 1 =
x x 0 f(x)
● Αν lim f(x)= ή , τότε lim | f(x)|=
x x 0 x x 0
● Αν lim f(x)= , τότε lim f(x) =
k
x x x x
0 0

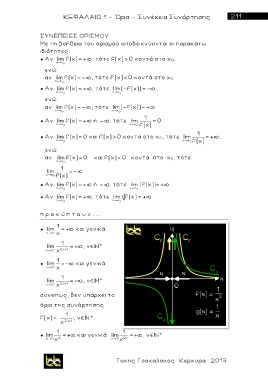
π ρ ο κ ύ π τ ο υ ν . . .

● lim 1 = + και γενικά
x 0 x

lim 1 = + , ν © *
x 0 x 2 1
1
● lim =- και γενικά
x 0 x
1
lim =- , ν © *
x 0 x 2 1

συνεπώς, δεν υπάρχει το

όριο της συνάρτησης
1
f(χ)= , ν © *
x 2 1

1 1
● lim =+ και γενικά lim = + , ν ©*
x 0 x 2 x 0 x 2

Τακης Τσακαλακος Κερκυρα 2017