Page 222 - chapter 1

222
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

Θ Ε Ω Ρ Ι Α ...

ΕΝΝΟΙΑ ΟΡΙΟΥ ΣΤΟ ΑΠΕΙΡΟ

Παρακάτω ο όρος “ τ ε ί ν ε ι σ τ ο + ( - ) “ θα σημαίνει
“ α υ ξ ά ν ε ι ( μ ε ι ώ ν ε τ α ι ) α π ε ρ ι ό ρ ι σ τ α “ .
Προσεγγίζουμε την έννοια του ορίου στο άπειρο μέσω της
γ ρ αφικής παράστασης μιας συνάρτησης.
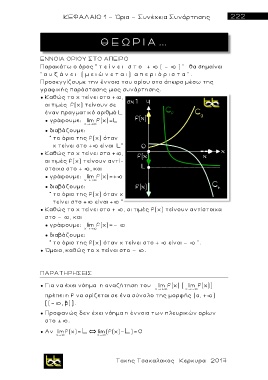
● Καθώς το x τείνει στο + ,
οι τιμές f(x) τ ε ίνουν σε
έναν πραγματικό αριθμό L, και
● γ ρ άφ ο υμε: lim f(x)=L
x +
● διαβάζουμε:
“ το όριο της f(x) όταν
x τ ε ίνει στο + είναι L”.

● Καθώς το x τείνει στο + ,
οι τιμές f(x) τείνουν αντί-
στοιχα στο + , και
● γ ρ άφ ο υμε: lim f(x)=+
x +
● διαβάζουμε:
“ το όριο της f(x) όταν x
τ ε ίνει στο + είναι + ”
● Καθώς το x τείνει στο + , οι τιμές f(x) τείνουν αντίστοιχα
στο - , και
● γ ρ άφ ο υμε: lim f(x)=-
x +
● διαβάζουμε:
“ το όριο της f(x) όταν x τείνει στο + είναι - ” .
● Όμοια, καθώς το x τείνει στο - .

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Για να έχει νόημα η αναζήτηση του lim f(x) [ lim f(x)]
x + x -
πρέπει η f να ορίζεται σε ένα σύνολο της μορφής (α, + )
[(- , β)].

● Προφανώς δεν έχει νόημα η έννοια των πλευρικών ορίων
στο ± .
● Αν lim f(x)=L` lim (f(x)-L )= 0
x x

Τακης Τσακαλακος Κερκυρα 2017