Page 314 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 314

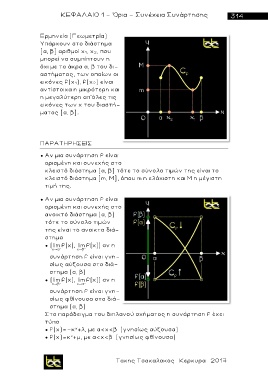
Ερμηνεία (Γεωμετρία )
Υπάρχουν στο διάστημα
[α, β] αριθμοί x 1, x 2, που
μπορεί να συμπίπτουν η

όχι με τα άκρα α, β του δι-
ασ τ ήμ α τος, των οποίων οι
εικόνες f(x 1), f(x 2) είναι
αντίστοιχα η μικρότερη και
η μεγαλύτερη απ’όλες τις
εικόνες των x του διασ τ ή-
ματος [α, β].

ΠΑΡΑΤΗΡΗΣΕΙΣ

● Αν μια συνάρτηση f είναι
ορισμένη και συνεχής στο
κλειστό διάστημα [α, β] τότε το σύνολο τιμών της είναι το
κλειστό διάστημα [m, M], όπου m η ελάχιστη και Μ η μέγιστη
τιμή της.

● Αν μια συνάρτηση f είναι
ορισμένη και συνεχής στο
ανοικτό διάστημα (α, β)
τότε το σύνολο τιμών

τ η ς είναι το ανοικτο διά-
στημα
● (lim f(x), lim f(x)) αν η
x x
συνάρτηση f είναι γνη-
σίως αύξουσα στο διά-
στημα (α, β)
● (lim f(x), lim f(x)) αν η
x x
συνάρτηση f είναι γνη-
σίως φθίνουσα στο διά-
στημα (α, β)
Στο παράδειγμα του διπλανού σχήματος η συνάρτηση f έχει
τύπ ο
● f(χ)=-κ + λ , με α<χ<β (γνησίως αύξουσα)
χ
● f(χ)=κ +μ, με α<χ<β (γνησίως φθίνουσα)
χ

Τακης Τσακαλακος Κερκυρα 2017