Page 334 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 334

2. ΣΥΝΔΥΑΣΤΙΚΗ
Δίνονται οι συναρτήσεις f,g : [0, 1] για τις οποίε ς
● Η συνάρτηση f είναι συνεχής στο πεδίο ορισμού της με
f(0)=e, f(1)=e και για κάθε χ [0, 1] ισχύει f(x)>0
2
● g(x)=lnf(x), για κάθε χ [0, 1]
Nα αποδείξετε ότ ι
3
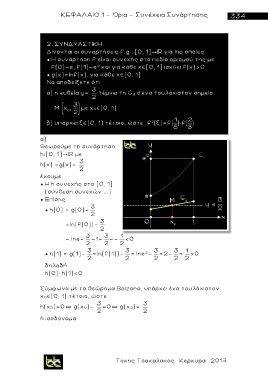
α) η ευθεία y= 2 τέμνει τη C g σ'ένα τουλάχιστον σημείο
3
Μ x , 2 με χ 0 (0, 1)
0
1 2
2
β) υπάρχει ξ (0, 1) τέτοιο, ώστε f (ξ)= f( )× f( )
5
5

α )
Θεωρούμε τη συνάρτηση
h:[0, 1] με
3
h(x) =g(x)-
2
έχουμε
● Η h συνεχής στο [0, 1]
(σύνθεση συνεχών ...)
● Επίσης
3
● h(0) = g(0)-
2
3
=ln(f(0))-
2
3 3 1
= lne- =1- =- <0
2 2 2
3 3 3 3 1
● h(1) = g(1)- =ln(f(1))- = lne - =2- = >0
2
2 2 2 2 2
δηλαδή

h(0) h(1)<0

Σύμφωνα με το θεώρημα Bolzano, υπάρχει ένα τουλάχιστον

χ 0 (0, 1) τέτοιο, ώστε
3 3
h(χ 0)=0` g(χ 0)- =0` g(χ 0)=
2 2
ή ισοδύναμα

Τακης Τσακαλακος Κερκυρα 2017