Page 338 - chapter 1

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης 338

4. ΣΥΝΔΥΑΣΤΙΚΗ
Έστω η συνάρτηση f: συνεχής στο 0 με f(0)=1, για
την οποία ισχύει
1
2
xf(x)+x συν x = ημαχ, α 0 για κάθε χ *
α) Να αποδείξετε ότι η συνάρτηση f είναι συνεχής
β) Να βρείτε το α

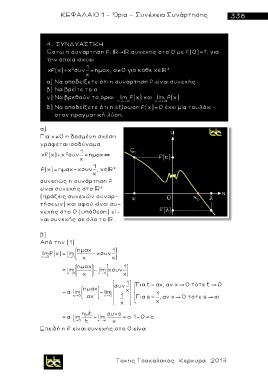
γ) Να βρεθούν τα όρια: lim f(x) και lim f(x)
x -
x +
δ) Να αποδείξετε ότι η εξίσωση f(χ)=0 έχει μία τουλάχ ι -
στον πραγματική λύση.

α )
Για χ 0 η δοσμένη σχέση
γ ρ άφεται ισοδύναμα
1
xf(x)+x συν = ημαχ`
2
x
1
f(x)= ημαχ-xσυν , χ * (1)
x
συνεπώς η συνάρτηση f
είναι συνεχής στο *
(πράξεις συνεχών συνα ρ -

τήσεων) και αφού είναι σ υ -
νεχής στο 0 (υπόθεση) εί-
ναι συνεχής σ ε όλο το .

β )
Από την (1)
ημαx 1
limf(x)= lim -xσυν
x 0 x 0 x x

ημαx 1
= lim - lim xσυν
x 0 x x 0 x

συν 1 Για t= αχ, αν χ 0 τότε t 0
ημαx x
= α lim - lim 1
x 0 αx x 0 1 Για s= , αν χ 0 τότε s
x χ

ημt συνs
= α× lim - lim = α× 1-0= α
t 0 t x s
Eπειδή η f είναι συνεχής στο 0 είναι

Τακης Τσακαλακος Κερκυρα 2017