Page 169 - Cambridge+Checkpoint+Mathematics+Coursebook+9

18.2 The graph of y = mx + c

18.2 The graph of y = mx + c

y
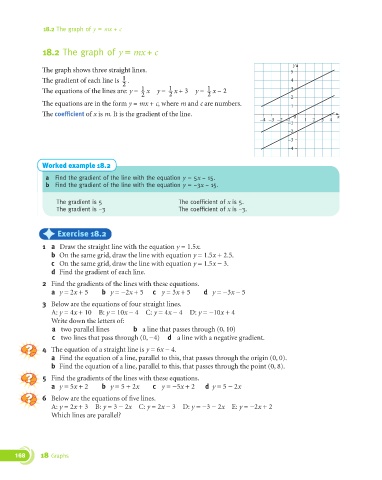
"e graph shows three straight lines. 5
1
"e gradient of each line is . 4
2
1
1
1
"e equations of the lines are: y = x y = x + 3 y = x − 2 3
2 2 2 2
"e equations are in the form y = mx + c, where m and c are numbers. 1
"e coefficient of x is m. It is the gradient of the line.
–4 –3 –2 –1 0 1 2 3 4 x
–1
–2
–3
–4

Worked example 18.2
a Find the gradient of the line with the equation y = 5x − 15.
b Find the gradient of the line with the equation y = −3x − 15.

The gradient is 5 The coefficient of x is 5.
The gradient is −3 The coefficient of x is −3.

) Exercise 18.2

1 a Draw the straight line with the equation y = 1.5x.
b On the same grid, draw the line with equation y = 1.5x + 2.5.
c On the same grid, draw the line with equation y = 1.5x − 3.
d Find the gradient of each line.
2 Find the gradients of the lines with these equations.
a y = 2x + 5 b y = −2x + 5 c y = 3x + 5 d y = −3x − 5
3 Below are the equations of four straight lines.
A: y = 4x + 10 B: y = 10x − 4 C: y = 4x − 4 D: y = −10x + 4
Write down the letters of:
a two parallel lines b a line that passes through (0, 10)
c two lines that pass through (0, −4) d a line with a negative gradient.
4 The equation of a straight line is y = 6x − 4.
a Find the equation of a line, parallel to this, that passes through the origin (0, 0).
b Find the equation of a line, parallel to this, that passes through the point (0, 8).
5 Find the gradients of the lines with these equations.
a y = 5x + 2 b y = 5 + 2x c y = −5x + 2 d y = 5 − 2x
6 Below are the equations of five lines.
A: y = 2x + 3 B: y = 3 − 2x C: y = 2x − 3 D: y = −3 − 2x E: y = −2x + 2
Which lines are parallel?

168 18 Graphs 18 Graphs