Page 156 - Echte wiskunde

144
P.W. Hemker
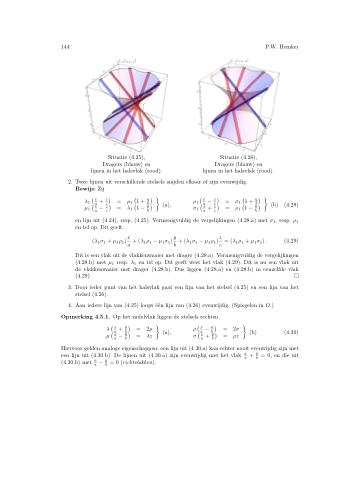
Situatie (4.25), Dragers (blauw) en lijnen in het halsvlak (rood).
Situatie (4.26), Dragers (blauw) en lijnen in het halsvlak (rood).
2. Twee lijnen uit verschillende stelsels snijden elkaar of zijn evenwijdig. Bewijs: Zij
λ (x+z) = μ (1+y)} ρ (x−z) = σ (1+y)}
1(a c) 1( b) (a), 1(a c) 1( b) (b) (4.28)
μ1 x−z = λ1 1−y σ1 x+z = ρ1 1−y acbacb
en lijn uit (4.24), resp. (4.25). Vermenigvuldig de vergelijkingen (4.28.a) met σ1, resp. ρ1 en tel op. Dit geeft:
(λ1 σ1 + μ1 ρ1 ) x + (λ1 ρ1 − μ1 σ1 ) y + (λ1 σ1 − μ1 ρ1 ) z = (λ1 ρ1 + μ1 σ1 ) . (4.29) abc
Dit is een vlak uit de vlakkenwaaier met drager (4.28.a). Vermenigvuldig de vergelijkingen (4.28.b) met μ1 resp. λ1 en tel op. Dit geeft weer het vlak (4.29). Dit is nu een vlak uit de vlakkenwaaier met drager (4.28.b). Dus liggen (4.28.a) en (4.28.b) in eenzelfde vlak (4.29).
3. Door ieder punt van het halsvlak gaat een lijn van het stelsel (4.25) en een lijn van het stelsel (4.26).
4. Aan iedere lijn van (4.25) loopt één lijn van (4.26) evenwijdig. (Spiegelen in O.)
Opmerking 4.5.1. Op het zadelvlak liggen de stelsels rechten
λ(x+y) = 2μ} ρ(x−y) = 2σ}
(a b) (a), (a b) (b) (4.30)
μ x − y = λz σ x + y = ρz ab ab
Hiervoor gelden analoge eigenschappen; een lijn uit (4.30.a) kan echter nooit evenwijdig zijn met
een lijn uit (4.30.b). De lijnen uit (4.30.a) zijn evenwijdig met het vlak a + y = 0, en die uit
(4.30.b) met a − y = 0 (richtvlakken). x b xb