Page 18 - Echte wiskunde

6 P.W. Hemker
is) moet je altijd eerst controleren of ze echt waar zijn. Als wiskundigen zo’n waarheid nagaan, zeggen ze dat ze de stelling bewijzen.
Om wiskunde te bedenken moet je eerst goede stellingen verzinnen en ze daarna bewijzen. Dat is precies wat we nu gaan doen in de meetkunde.
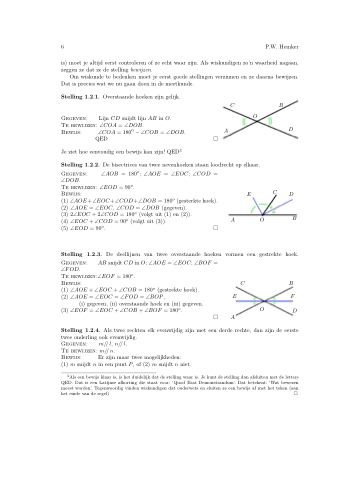
Stelling 1.2.1. Overstaande hoeken zijn gelijk.
Gegeven: Lijn CD snijdt lijn AB in O.
Te bewijzen: ∠COA = ∠DOB.
Bewijs: ∠COA = 1800 − ∠COB = ∠DOB.
QED
Je ziet hoe eenvoudig een bewijs kan zijn! QED3
CB O
Stelling 1.2.2. De bisectrices van twee nevenhoeken staan loodrecht op elkaar.
Gegeven: ∠AOB = 180o; ∠AOE = ∠EOC; ∠COD =
∠DOB.
Te bewijzen: ∠EOD = 90o.
Bewijs: ECD (1) ∠AOE+∠EOC+∠COD+∠DOB = 180o (gesterkte hoek).
A
D
(2) ∠AOE = ∠EOC, ∠COD = ∠DOB (gegeven). (3) 2∠EOC + 2∠COD = 180o (volgt uit (1) en (2)). (4) ∠EOC + ∠COD = 90o (volgt uit (3)).
(5) ∠EOD = 90o.
AO
B
Stelling 1.2.3. De deellijnen van twee overstaande hoeken vormen een gestrekte hoek.
Gegeven: AB snijdt CD in O; ∠AOE = ∠EOC; ∠BOF =
∠FOD.
Te bewijzen:∠EOF = 180o.
Bewijs: C (1) ∠AOE + ∠EOC + ∠COB = 180o (gestrekte hoek).
(2) ∠AOE = ∠EOC = ∠FOD = ∠BOP, E (i) gegeven, (ii) overstaande hoek en (iii) gegeven.
(3) ∠EOF = ∠EOC +∠COB +∠BOF = 180o.
A
Stelling 1.2.4. Als twee rechten elk evenwijdig zijn met een derde rechte, dan zijn de eerste twee onderling ook evenwijdig.
Gegeven: m// l, n// l.
Te bewijzen: m// n.
Bewijs: Er zijn maar twee mogelijkheden:
(1) m snijdt n in een punt P, of (2) m snijdt n niet.
3Als een bewijs klaar is, is het duidelijk dat de stelling waar is. Je kunt de stelling dan afsluiten met de letters QED. Dat is een Latijnse afkorting die staat voor: ‘Quod Erat Demonstrandum’. Dat betekent: ‘Wat bewezen moest worden’. Tegenwoordig vinden wiskundigen dat ouderwets en sluiten ze een bewijs af met het teken (aan het einde van de regel) .
B F
O D