Page 48 - Echte wiskunde
P. 48
36 P.W. Hemker
1.11.2 De stellingen van Menelaos en De Ceva
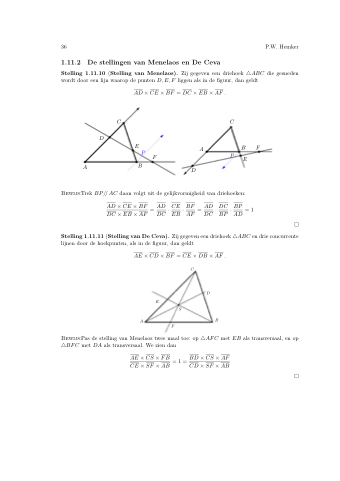
Stelling 1.11.10 (Stelling van Menelaos). Zij gegeven een driehoek △ABC die gesneden wordt door een lijn waarop de punten D,E,F liggen als in de figuur, dan geldt
AD×CE×BF =DC×EB×AF.
CC
D
A
E
P
F B
A
D
P
BF E
Bewijs:Trek BP // AC daan volgt uit de gelijkvormigheid van driehoeken: AD×CE×BF =AD·CE·BF =AD·DC·BP =1
DC × EB × AF DC EB AF DC BP AD
Stelling 1.11.11 (Stelling van De Ceva). Zij gegeven een driehoek △ABC en drie concurrente lijnen door de hoekpunten, als in de figuur, dan geldt
AE×CD×BF =CE×DB×AF. C
A
E
D
B
S
F
Bewijs:Pas de stelling van Menelaos twee maal toe: op △AFC met EB als transversaal, en op
△BFC met DA als transversaal. We zien dan
AE×CS×FB =1= BD×CS×AF CE × SF × AB CD × SF × AB