Page 15 - Math SL HB Sem 3

The quartiles (lower, upper quartiles and the median) and percentiles (for ah percentile, it is the value
below which n% of the data lie) can be easily estimated from the cumulative frequency graph, as

demonstrated below:
_I

I
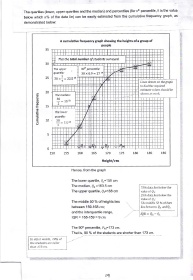
A cumulative frequency graph showing the heights of a group of
people
35 -T-rT-rT-TTT-rTT-r -TTI-
-rt-T-
This the total numbet ol students suNeyed atl I
30
I
The upper 90'h percentile:
quortile: 30x0.9=27tn
25 lo x1 = zz.s,h
Lines drawn on the graph
to find the required
estifiate values should be
20 shown as work
The medion:
c tttlttt
J a=1.,n
(t
o) 2
15
o
The lower
3 quottile:
E 10- 30
)
_:.7<tn
I 4"'
5

0
150 155 160 165 r70 L75 180 185 190

HeiBht/cm

Hence, from the graph

The lower quartile, Qr='1 59 cm
The median, Qz =163.5 cm
75ok data lies below the
The upper quartile, 0s=168 cm value of Qi
250/0 data lies below the
value of Q;
The middle 50 % of heights lies
The iddle 50 Yo ofdata
between 159-168 cm; lies between Q3 andQr.
and the interquartile range,
IQR=Q3-Q1
IQR = 168-159 = 9 cm

The 90b percentile, Pro=173 cm.
That is, 90 % of the students are shorter than 173 cm.
In otherwords, 100/0 of
the st.|dents are taller
than 773 cm.

t1