Page 68 - Math SL HB Sem 2

Kolej MARA Seremban Mathematics IB High Level
Core : Vectors

Vectors In 3-Dimensional Space

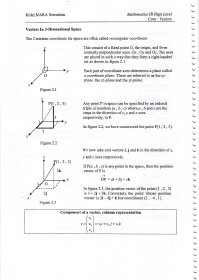
The Cartesian coordinate for space are often called rectangular coordinate .

This consist ofa fixed point O, the origin, and three
mutually perpendicular axes, O.r , Oy and Oz. The axes
are placed in such a way that they form a right-handed
set as shown in figure 2.1.

v Each pair of coordinate axes determines a plane called
o a coordinate plan e. These are referred to as the.r/-
plane, the xz-plane and the yz-plane.
x
Figure 2.1

P(1 ,2 ,3) Any point P in space can be specified by an ordered
triple of numbers (a 6, c) where a ,b and c are the
,
steps in the direction ofx, y and z axes
3 respectively, to P.
v
ln figore 2.2, we have constructed the point P(l ,2 ,3).
2
x
Figre 2.2

We now take unit vectors i, j and k in the direction of -r,
z y and z axes respectively.
I ,2,3)
lfP(a , b, c) is any point in the space, then the position
3k vector ofP is
-)
v OP:ai+bj+ck
o
), In figure 2.3, the position vector olthe point (1 2 , 3)
,
2i is i+ 2j + 3k. Conversely, the point whose position
x vector is 2i 4i + k has coordinates (2 , -4 , 1).
-
Figure 2.3

Component of a vector, column representation
yr
v2 =vri +vrj + vrk
y3