Page 93 - J. C. Turner "History and Science of Knots"

82 History and Science of Knots

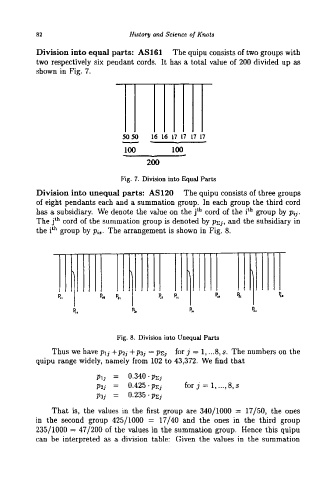
Division into equal parts : AS161 The quipu consists of two groups with
two respectively six pendant cords. It has a total value of 200 divided up as
shown in Fig. 7.

5050 16 16 17 17 17 17
100 100
200

Fig. 7. Division into Equal Parts
Division into unequal parts : AS120 The quipu consists of three groups
of eight pendants each and a summation group. In each group the third cord
has a subsidiary. We denote the value on the jth cord of the ith group by pij.
The jth cord of the summation group is denoted by prj, and the subsidiary in
the ith group by is. The arrangement is shown in Fig. 8.

n N

P. Pie P=1 P. P. P,
Pi. PU Ph PE.

Fig. 8. Division into Unequal Parts
Thus we have Plj +p2j +p3j = P j for j = 1, ...8, s. The numbers on the
quipu range widely, namely from 102 to 43,372. We find that

Pi j = 0.340 •prj
= 0.425 • pEj for j = 1, ..., 8, s
P2j
= 0.235 • prj
P3j
That is, the values in the first group are 340/1000 = 17/50, the ones
in the second group 425/1000 = 17/40 and the ones in the third group
235/1000 = 47/200 of the values in the summation group. Hence this quipu
can be interpreted as a division table: Given the values in the summation