Page 95 - Maxwell House

NEOCLASSICAL THEORY OF INTERACTION 75

Here the constant = / is the metal conductivity and () = 1. In case of copper
2
′

the ratio / ≅ 3.8 ⋅ 10 −17 (see above) and = 1.602 ⋅ 10 −19 . Therefore, = 6.75 ⋅

10 −22 . If so, we can roughly estimate that the average number of conductivity electrons in
bulk copper with = 5.85 ⋅ 10 [S/m] is equal to = 8.66 ⋅ 10 [m ] (!) or almost 90
-3
7
28
octillions. Meanwhile, an octillion is a billion billion billions!! For contrast, our sun mass is
around 2 octillion tons only. All the oceans on Earth contain much less or about 3.25 ⋅ 10
25
drops of water, plus or minus several billions (assuming 25 drops per 1 cm ).
3
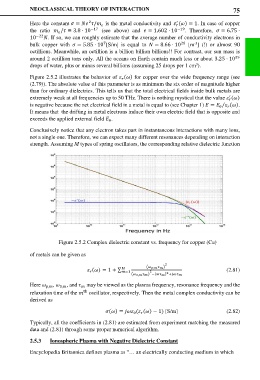
Figure 2.5.2 illustrates the behavior of () for copper over the wide frequency range (see

(2.79)). The absolute value of this parameter is as minimum the six order of magnitude higher
than for ordinary dielectrics. This tells us that the total electrical fields inside bulk metals are
extremely weak at all frequencies up to 50 THz. There is nothing mystical that the value ()
′

is negative because the net electrical field in a metal is equal to (see Chapter 1) = ()⁄ .
0
It means that the drifting in metal electrons induce their own electric field that is opposite and
exceeds the applied external field .
0
Conclusively notice that any electron takes part in instantaneous interactions with many ions,
not a single one. Therefore, we can expect many different resonances depending on interaction
strength. Assuming M types of spring oscillators, the corresponding relative dielectric function

Figure 2.5.2 Complex dielectric constant vs. frequency for copper (Cu)
of metals can be given as

2
() = 1 + ∑ � , � (2.81)
2
=1

� 0, � −( ) 2 +
Here , , 0, , and may be viewed as the plasma frequency, resonance frequency and the

relaxation time of the oscillator, respectively. Then the metal complex conductivity can be
th
derived as
() = ( () − 1) [S/m] (2.82)
0

Typically, all the coefficients in (2.81) are estimated from experiment matching the measured
data and (2.81) through some proper numerical algorithm.
2.5.3 Ionospheric Plasma with Negative Dielectric Constant
Encyclopedia Britannica defines plasma as “… an electrically conducting medium in which