Page 137 - КАНОНЫ ЕДИНОГО ЗНАНИЯ-издание 2
P. 137
136 | «Междисциплинарный синтез Веры и Знания», © , 2013
11.4. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ МОДЕЛИ РАВНОВЕСИЯ
Существует два основных типа моделей: графические и
аналитические. Декарт показал, что любой геометрический
результат может быть представлен в аналитическом виде. Точки
геометрических фигур можно представить нанесёнными на
координатную сетку, на которой положение точки определяется
парой чисел (х, у). Любое свойство, встречающееся в геометрии,
может быть переведено на язык алгебраических соотношений
между координатами х и у различных точек. Ценность
взаимосвязи между геометрическими и алгебраическими
формами заключается, прежде всего, в том, что она позволяет
переходить от алгебры к геометрии и наоборот. Очень часто
смысл алгебраического результата виден гораздо лучше, если его
перевести на язык геометрии.
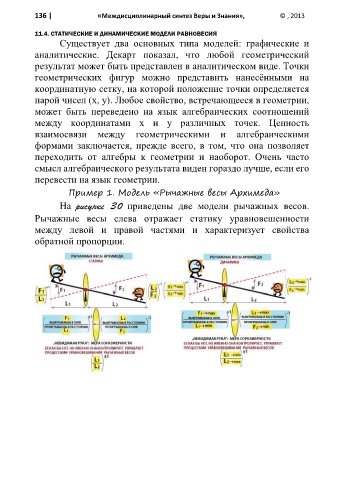
Пример 1. Модель «Рычажные весы Архимеда»
На рисунке 30 приведены две модели рычажных весов.
Рычажные весы слева отражает статику уравновешенности
между левой и правой частями и характеризует свойства
обратной пропорции.