Page 104 - Mechatronics with Experiments
P. 104
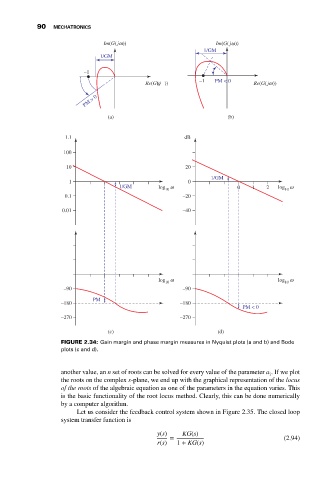
90 MECHATRONICS
Im(G(j ))ω Im(G(j ))
ω
1/GM
1/GM
–1
ω
ω
Re(G(j )) –1 PM < 0 Re(G(j ))
PM > 0
(a) (b)
1.1 dB
100
10 20
1/GM
1 0
1/GM log ω 0 1 2 log ω
10 10
0.1 –20
0.01 –40
log ω log ω
10 10
–90 –90
PM
–180 –180
PM < 0
–270 –270
(c) (d)
FIGURE 2.34: Gain margin and phase margin measures in Nyquist plots (a and b) and Bode
plots (c and d).
another value, an n set of roots can be solved for every value of the parameter a .Ifweplot
i
the roots on the complex s-plane, we end up with the graphical representation of the locus
of the roots of the algebraic equation as one of the parameters in the equation varies. This
is the basic functionality of the root locus method. Clearly, this can be done numerically
by a computer algorithm.
Let us consider the feedback control system shown in Figure 2.35. The closed loop
system transfer function is
y(s) KG(s)
= (2.94)
r(s) 1 + KG(s)