Page 109 - Mechatronics with Experiments

CLOSED LOOP CONTROL 95
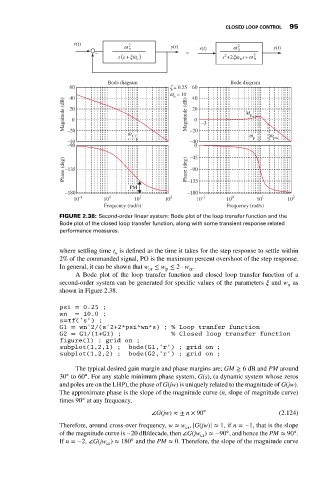
r(t) 2
ω n y(t) r(t) ω 2 y(t)
_ = n 2
s s + ξω n s +2 ξω s ω n
2
+
n
Bode diagram Bode diagram
60 ζ = 0.25 60
ω n = 10 40
40
Magnitude (dB) 20 Magnitude (dB) 20 0 –3 M p

0
–20
ω LT –20 ω ω
–40 –40 p pw
–90 0
Phase (deg) –135 Phase (deg) –45
–90

PM –135
–180 –180
10 –1 10 0 10 1 10 2 10 –1 10 0 10 1 10 2
Frequency (rad/s) Frequency (rad/s)
FIGURE 2.38: Second-order linear system: Bode plot of the loop transfer function and the
Bode plot of the closed loop transfer function, along with some transient response related
performance measures.

where settling time t is defined as the time it takes for the step response to settle within
s
2% of the commanded signal, PO is the maximum percent overshoot of the step response.
In general, it can be shown that w ≤ w ≤ 2 ⋅ w .
cr
p
cr
A Bode plot of the loop transfer function and closed loop transfer function of a
second-order system can be generated for specific values of the parameters and w as
n
shown in Figure 2.38.
psi = 0.25 ;
wn = 10.0 ;
s=tf(’s’) ;
G1 = wnˆ2/(sˆ2+2*psi*wn*s) ; % Loop tranfer function
G2 = G1/(1+G1) ; % Closed loop transfer function
figure(1) ; grid on ;
subplot(1,2,1) ; bode(G1,’r’) ; grid on ;
subplot(1,2,2) ; bode(G2,’r’) ; grid on ;

The typical desired gain margin and phase margins are; GM ≥ 6 dB and PM around
◦
◦
30 to 60 . For any stable minimum phase system, G(s), (a dynamic system whose zeros
and poles are on the LHP), the phase of G(jw) is uniquely related to the magnitude of G(jw).
The approximate phase is the slope of the magnitude curve (n, slope of magnitude curve)
◦
times 90 at any frequency,
∠G(jw) ≈± n × 90 ◦ (2.124)

Therefore, around cross-over frequency, w ≈ w , |G(jw)| ≈ 1, if n =−1, that is the slope
cr
◦
◦
of the magnitude curve is −20 dB/decade, then ∠G(jw ) ≈−90 , and hence the PM ≈ 90 .
cr
◦
If n =−2, ∠G(jw ) ≈ 180 and the PM ≈ 0. Therefore, the slope of the magnitude curve
cr