Page 192 - Mechatronics with Experiments

178 MECHATRONICS
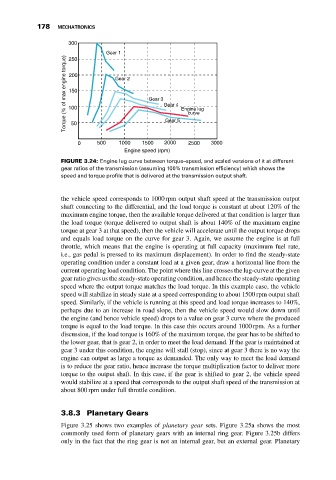
300
Gear 1
Torque (% of max engine torque) 100 Gear 2 Gear 3 Gear 4 Engine lug
250
200

150

curve
Gear 5
50

0 500 1000 1500 2000 2500 3000
Engine speed (rpm)
FIGURE 3.24: Engine lug curve between torque–speed, and scaled versions of it at different
gear ratios of the transmission (assuming 100% transmission efficiency) which shows the
speed and torque profile that is delivered at the transmission output shaft.

the vehicle speed corresponds to 1000 rpm output shaft speed at the transmission output
shaft connecting to the differential, and the load torque is constant at about 120% of the
maximum engine torque, then the available torque delivered at that condition is larger than
the load torque (torque delivered to output shaft is about 140% of the maximum engine
torque at gear 3 at that speed), then the vehicle will accelerate until the output torque drops
and equals load torque on the curve for gear 3. Again, we assume the engine is at full
throttle, which means that the engine is operating at full capacity (maximum fuel rate,
i.e., gas pedal is pressed to its maximum displacement). In order to find the steady-state
operating condition under a constant load at a given gear, draw a horizontal line from the
current operating load condition. The point where this line crosses the lug-curve at the given
gear ratio gives us the steady-state operating condition, and hence the steady-state operating
speed where the output torque matches the load torque. In this example case, the vehicle
speed will stabilize in steady state at a speed corresponding to about 1500 rpm output shaft
speed. Similarly, if the vehicle is running at this speed and load torque increases to 140%,
perhaps due to an increase in road slope, then the vehicle speed would slow down until
the engine (and hence vehicle speed) drops to a value on gear 3 curve where the produced
torque is equal to the load torque. In this case this occurs around 1000 rpm. As a further
discussion, if the load torque is 160% of the maximum torque, the gear has to be shifted to
the lower gear, that is gear 2, in order to meet the load demand. If the gear is maintained at
gear 3 under this condition, the engine will stall (stop), since at gear 3 there is no way the
engine can output as large a torque as demanded. The only way to meet the load demand
is to reduce the gear ratio, hence increase the torque multiplication factor to deliver more
torque to the output shaft. In this case, if the gear is shifted to gear 2, the vehicle speed
would stabilize at a speed that corresponds to the output shaft speed of the transmission at
about 800 rpm under full throttle condition.

3.8.3 Planetary Gears

Figure 3.25 shows two examples of planetary gear sets. Figure 3.25a shows the most
commonly used form of planetary gears with an internal ring gear. Figure 3.25b differs
only in the fact that the ring gear is not an internal gear, but an external gear. Planetary