Page 187 - Mechatronics with Experiments

MECHANISMS FOR MOTION TRANSMISSION 173

Resistance resistance aero
Total

Aerodynamic F F roll
resistance
Gradient
resistance
Fgrade =
mg m g sin( ) θ
Rolling
resistance
Vehicle speed
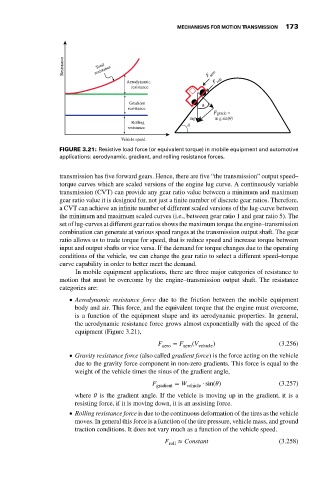
FIGURE 3.21: Resistive load force (or equivalent torque) in mobile equipment and automotive
applications: aerodynamic, gradient, and rolling resistance forces.

transmission has five forward gears. Hence, there are five “the transmission” output speed–
torque curves which are scaled versions of the engine lug curve. A continuously variable
transmission (CVT) can provide any gear ratio value between a minimum and maximum
gear ratio value it is designed for, not just a finite number of discrete gear ratios. Therefore,
a CVT can achieve an infinite number of different scaled versions of the lug-curve between
the minimum and maximum scaled curves (i.e., between gear ratio 1 and gear ratio 5). The
set of lug-curves at different gear ratios shows the maximum torque the engine–transmission
combination can generate at various speed ranges at the transmission output shaft. The gear
ratio allows us to trade torque for speed, that is reduce speed and increase torque between
input and output shafts or vice versa. If the demand for torque changes due to the operating
conditions of the vehicle, we can change the gear ratio to select a different speed–torque
curve capability in order to better meet the demand.
In mobile equipment applications, there are three major categories of resistance to
motion that must be overcome by the engine–transmission output shaft. The resistance
categories are:
Aerodynamic resistance force due to the friction between the mobile equipment

body and air. This force, and the equivalent torque that the engine must overcome,
is a function of the equipment shape and its aerodynamic properties. In general,
the aerodynamic resistance force grows almost exponentially with the speed of the
equipment (Figure 3.21),

F = F (V ) (3.256)
aero aero vehicle
Gravity resistance force (also called gradient force) is the force acting on the vehicle
due to the gravity force component in non-zero gradients. This force is equal to the
weight of the vehicle times the sinus of the gradient angle,
F = W ⋅ sin( ) (3.257)
gradient vehicle
where is the gradient angle. If the vehicle is moving up in the gradient, it is a
resisting force, if it is moving down, it is an assisting force.
Rolling resistance force is due to the continuous deformation of the tires as the vehicle

moves. In general this force is a function of the tire pressure, vehicle mass, and ground
traction conditions. It does not vary much as a function of the vehicle speed.
F roll ≈ Constant (3.258)