Page 182 - Mechatronics with Experiments

168 MECHATRONICS
Hence, the force–torque relationship between the tool and joint variables is
T
Torque = J ⋅ Force (3.223)
and the inverse relationship is
T −1
Force = (J ) ⋅ Torque (3.224)
Notice that at the singular configurations (geometric singularities) of the mechanism, those
configuration of the mechanism at which the inverse of the Jacobian matrix does not exist,
there are some force directions at the tool which do not result in any change in the axes,
torques. They only result in reaction forces in the linkage structure, but not in the actuation
axes. Another interpretation of this result is that there are some directions of tool motion
where we cannot generate force no matter what combination of torques are applied at the
joints.
There are different methods for the calculation of the Jacobian matrix for a mechanism
[9,10]. The inverse Jacobian matrix can be either obtained analytically in symbolic form
or calculated numerically off-line or on-line (in real-time). However, real-time numerical
inverse calculations present a problem both in terms of the computational load and also
the possible numerical stability problems around the singularities of the mechanism. The
decision regarding the Jacobian matrix and its inverse computations in real-time should be
made on a mechanism by mechanism basis.

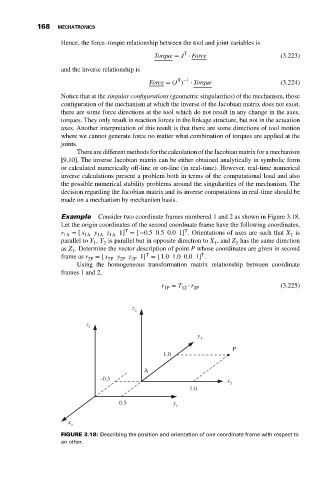
Example Consider two coordinate frames numbered 1 and 2 as shown in Figure 3.18.
Let the origin coordinates of the second coordinate frame have the following coordinates,
T
T
r 1A = [ x 1A y 1A z 1A 1] = [ −0.50.50.01] . Orientations of axes are such that X is
2
parallel to Y , Y is parallel but in opposite direction to X , and Z has the same direction
1
2
1
2
as Z . Determine the vector description of point P whose coordinates are given in second
1
T
T
frame as r 2P = [ x 2P y 2P z 2P 1] = [1.01.00.01] .
Using the homogeneous transformation matrix relationship between coordinate
frames 1 and 2,
r = T ⋅ r (3.225)
1P 12 2P
z
2
z
1
y
2
P
1.0
A
–0.5 x 2
1.0

0.5 y 1

x
1
FIGURE 3.18: Describing the position and orientation of one coordinate frame with respect to
an other.