Page 92 - Mechatronics with Experiments

78 MECHATRONICS
u(t) y(t)

L .T . I

t t

δ (t) h(t)

t t

s-plane

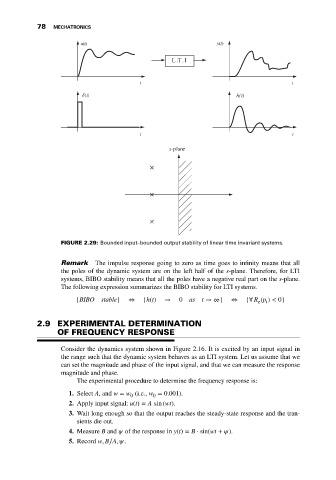
FIGURE 2.29: Bounded input–bounded output stability of linear time invariant systems.

Remark The impulse response going to zero as time goes to infinity means that all
the poles of the dynamic system are on the left half of the s-plane. Therefore, for LTI
systems, BIBO stability means that all the poles have a negative real part on the s-plane.
The following expression summarizes the BIBO stability for LTI systems.
{BIBO stable} ⇔ {h(t) → 0 as t → ∞} ⇔ {∀ R (p ) < 0}
e i

2.9 EXPERIMENTAL DETERMINATION
OF FREQUENCY RESPONSE

Consider the dynamics system shown in Figure 2.16. It is excited by an input signal in
the range such that the dynamic system behaves as an LTI system. Let us assume that we
can set the magnitude and phase of the input signal, and that we can measure the response
magnitude and phase.
The experimental procedure to determine the frequency response is:

1. Select A, and w = w (i.e., w = 0.001).
0 0
2. Apply input signal: u(t) = A sin (wt).
3. Wait long enough so that the output reaches the steady-state response and the tran-
sients die out.
4. Measure B and of the response in y(t) = B ⋅ sin(wt + ).
5. Record w, B∕A, .