Page 23 - modul trigonometri_Neat

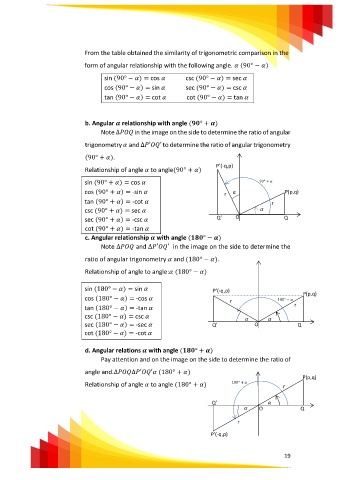
From the table obtained the similarity of trigonometric comparison in the

form of angular relationship with the following angle. (90° − )
sin (90° − ) = cos csc (90° − ) = sec

cos (90° − ) = sin sec (90° − ) = csc
tan (90° − ) = cot cot (90° − ) = tan

b. Angular relationship with angle ( ° + )
Note ∆ in the image on the side to determine the ratio of angular

trigonometry and ∆ ′ ′ to determine the ratio of angular trigonometry

(90° + ).
P’(-q,p)
Relationship of angle to angle(90° + )
sin (90° + ) = cos 90° +
cos (90° + ) = -sin r P(p,q)

tan (90° + ) = -cot r
csc (90° + ) = sec
sec (90° + ) = -csc Q’ O Q
cot (90° + ) = -tan
c. Angular relationship with angle ( ° − )
Note ∆ and ∆ ′ ′ in the image on the side to determine the

ratio of angular trigonometry and (180° − ).

Relationship of angle to angle: (180° − )

sin (180° − ) = sin P’(-q,p)
P(p,q)
cos (180° − ) = -cos r 180° −
tan (180° − ) = -tan r
csc (180° − ) = csc
sec (180° − ) = -sec Q’ O Q
cot (180° − ) = -cot

d. Angular relations with angle ( ° + )
Pay attention and on the image on the side to determine the ratio of

angle and.∆ ∆ ′ ′ (180° + )
P(p,q)
Relationship of angle to angle (180° + ) 180° + r

Q’
O Q

r

P’(-q,p)

19