Page 4 - logaritmos
P. 4
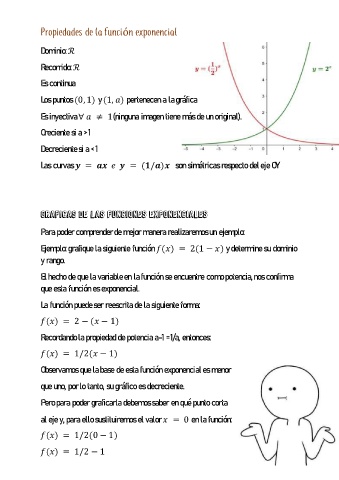
Propiedades de la función exponencial
Dominio: ℛ
Recorrido: ℛ
Es continua
Los puntos (0,1) y (1, ) pertenecen a la gráfica
Es inyectiva ∀ ≠ 1(ninguna imagen tiene más de un original).
Creciente si a > 1
Decreciente si a < 1
Las curvas = = ( / ) son simétricas respecto del eje OY
GRAFICAS DE LAS FUNCIONES EXPONENCIALES
Para poder comprender de mejor manera realizaremos un ejemplo:
Ejemplo: grafique la siguiente función ( ) = 2(1 − ) y determine su dominio
y rango.
El hecho de que la variable en la función se encuentre como potencia, nos confirma
que esta función es exponencial.
La función puede ser reescrita de la siguiente forma:
( ) = 2 − ( − 1)
Recordando la propiedad de potencia a-1 = 1/a, entonces:
( ) = 1/2( − 1)
Observamos que la base de esta función exponencial es menor
que uno, por lo tanto, su gráfico es decreciente.
Pero para poder graficarla debemos saber en qué punto corta
al eje y, para ello sustituiremos el valor = 0 en la función:
( ) = 1/2(0 − 1)
( ) = 1/2 − 1