Page 192 - Most-Essential-Learning-Competencies-Matrix-LATEST-EDITION-FROM-BCD

192

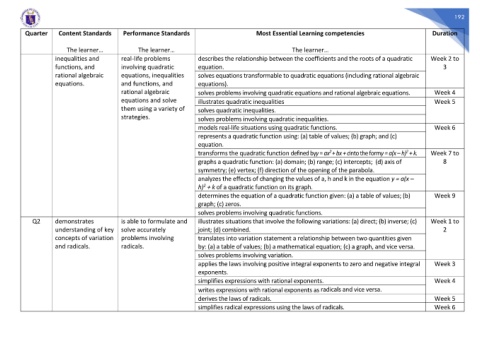
Quarter Content Standards Performance Standards Most Essential Learning competencies Duration

The learner… The learner… The learner…
inequalities and real-life problems describes the relationship between the coefficients and the roots of a quadratic Week 2 to
functions, and involving quadratic equation. 3
rational algebraic equations, inequalities solves equations transformable to quadratic equations (including rational algebraic
equations. and functions, and equations).
rational algebraic solves problems involving quadratic equations and rational algebraic equations. Week 4
equations and solve illustrates quadratic inequalities Week 5
them using a variety of solves quadratic inequalities.
strategies. solves problems involving quadratic inequalities.
models real-life situations using quadratic functions. Week 6
represents a quadratic function using: (a) table of values; (b) graph; and (c)
equation.
2
2
transforms the quadratic function defined byy = ax + bx + cinto the formy = a(x – h) + k. Week 7 to
graphs a quadratic function: (a) domain; (b) range; (c) intercepts; (d) axis of 8
symmetry; (e) vertex; (f) direction of the opening of the parabola.
analyzes the effects of changing the values of a, h and k in the equation y = a(x –
2
h) + k of a quadratic function on its graph.
determines the equation of a quadratic function given: (a) a table of values; (b) Week 9
graph; (c) zeros.
solves problems involving quadratic functions.
Q2 demonstrates is able to formulate and illustrates situations that involve the following variations: (a) direct; (b) inverse; (c) Week 1 to
understanding of key solve accurately joint; (d) combined. 2
concepts of variation problems involving translates into variation statement a relationship between two quantities given
and radicals. radicals. by: (a) a table of values; (b) a mathematical equation; (c) a graph, and vice versa.
solves problems involving variation.
applies the laws involving positive integral exponents to zero and negative integral Week 3
exponents.
simplifies expressions with rational exponents. Week 4
writes expressions with rational exponents as radicals and vice versa.
derives the laws of radicals. Week 5
simplifies radical expressions using the laws of radicals. Week 6