Page 34 - E-MODUL INTERAKTIF MATERI PROGRAM LINEAR BERBANTUAN LIVEWORKSHEETS DENGAN PENDEKATAN DISCOVERY LEARNING

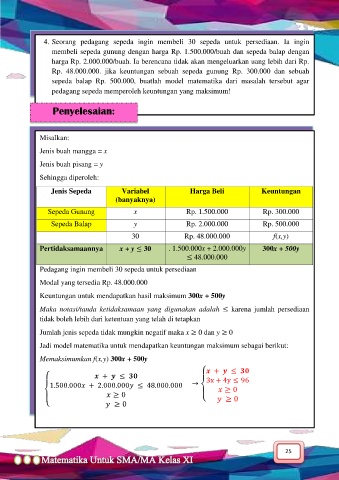
4. Seorang pedagang sepeda ingin membeli 30 sepeda untuk persediaan. Ia ingin
membeli sepeda gunung dengan harga Rp. 1.500.000/buah dan sepeda balap dengan
harga Rp. 2.000.000/buah. Ia berencana tidak akan mengeluarkan uang lebih dari Rp.

Rp. 48.000.000. jika keuntungan sebuah sepeda gunung Rp. 300.000 dan sebuah

sepeda balap Rp. 500.000, buatlah model matematika dari masalah tersebut agar

pedagang sepeda memperoleh keuntungan yang maksimum!

Penyelesaian:

Misalkan:

Jenis buah mangga = x

Jenis buah pisang = y

Sehingga diperoleh:

Jenis Sepeda Variabel Harga Beli Keuntungan

(banyaknya)

Sepeda Gunung x Rp. 1.500.000 Rp. 300.000

Sepeda Balap y Rp. 2.000.000 Rp. 500.000

30 Rp. 48.000.000 f(x,y)

Pertidaksamaannya x + y ≤ 30 . 1.500.000x + 2.000.000y 300x + 500y

≤ 48.000.000
Pedagang ingin membeli 30 sepeda untuk persediaan

Modal yang tersedia Rp. 48.000.000

Keuntungan untuk mendapatkan hasil maksimum 300x + 500y

Maka notasi/tanda ketidaksamaan yang digunakan adalah ≤ karena jumlah persediaan

tidak boleh lebih dari ketentuan yang telah di tetapkan

Jumlah jenis sepeda tidak mungkin negatif maka x ≥ 0 dan y ≥ 0

Jadi model matematika untuk mendapatkan keuntungan maksimum sebagai berikut:

Memaksimumkan f(x,y) 300x + 500y

+ ≤
+ ≤ 3x + 4y ≤ 96
1.500.000 + 2.000.000 ≤ 48.000.000 →
≥ 0
≥ 0 ≥ 0
≥ 0

25