Page 82 - Cuaderno de Activiades Tomo II

Capítulo 20 Geometría analítica II

INDICACIONES

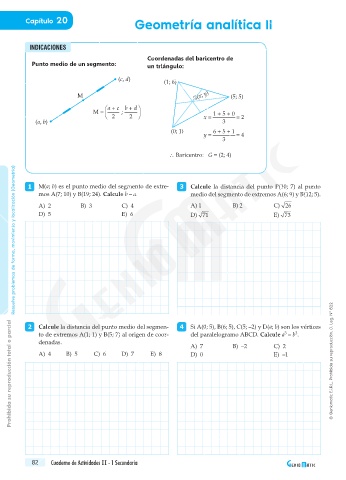
Coordenadas del baricentro de
Punto medio de un segmento: un triángulo:

(c, d)
(1; 6)
M G (x; y) (5; 5)

a + c b + d
M = ; 1 + 5 + 0
2 2 x = = 2
(a, b) 3
(0; 1) 6 + 5 + 1
y = = 4
3

\ Baricentro: G = (2; 4)

Resuelve problemas de forma, movimiento y localización (Geometría)

1 M(a; b) es el punto medio del segmento de extre- 3 Calcule la distancia del punto P(10; 7) al punto
mos A(7; 10) y B(19; 24). Calcule b – a. medio del segmento de extremos A(6; 9) y B(12; 5).
A) 2 B) 3 C) 4 A) 1 B) 2 C) 26
D) 5 E) 6 D) 71 E) 73

Prohibida su reproducción total o parcia l
2 Calcule la distancia del punto medio del segmen- 4 Si A(0; 5), B(6; 5), C(5; –2) y D(a; b) son los vértices
3
3
to de extremos A(1; 1) y B(5; 7) al origen de coor- del paralelogramo ABCD. Calcule a – b .
denadas.
A) 7 B) –2 C) 2
A) 4 B) 5 C) 6 D) 7 E) 8 D) 0 E) –1  Geniomatic E.I.R.L. Prohibida su reproducción. D. Leg. N° 822

82 Cuaderno de Actividades II - 1 Secundaria