Page 42 - Nature Of Space And Time

In these one sends particles in from in nity and observes what comes out again to in nity.
All measurements are made at in nity where one has a
at background metric and one
can interpret small
uctuations in the elds as particles in the usual way. One doesn't
ask what happens in the interaction region in the middle. That is why one does a path
integral over all possible histories for the interaction region, that is, over all asymptotically

Euclidean metrics.
However, in cosmology one is interested in measurements that are made in a nite
region rather than at in nity. We are on the inside of the universe not looking in from the

outside. To see what di erence this makes let us rst suppose that the path integral for
cosmology is to be taken over all asymptotically Euclidean metrics.

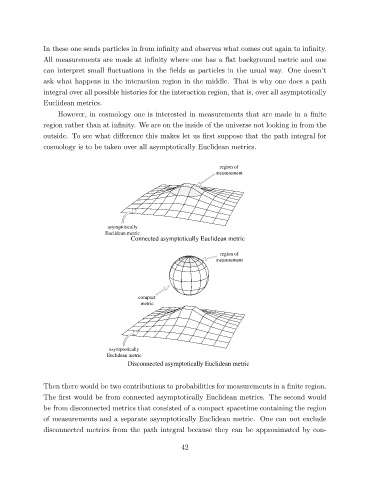
region of
measurement

asymptotically
Euclidean metric
Connected asymptotically Euclidean metric

region of
measurement

compact
metric

asymptotically
Euclidean metric
Disconnected asymptotically Euclidean metric

Then there would be two contributions to probabilities for measurements in a nite region.
The rst would be from connected asymptotically Euclidean metrics. The second would

be from disconnected metrics that consisted of a compact spacetime containing the region
of measurements and a separate asymptotically Euclidean metric. One can not exclude
disconnected metrics from the path integral because they can be approximated by con-

42