Page 47 - Nature Of Space And Time
P. 47
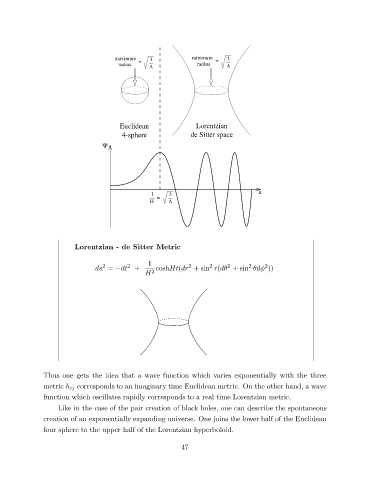
maximum 3 minimum = 3
radius = radius
L L
Euclidean Lorentzian
4-sphere de Sitter space
Y
a
1 3
=
H L
Lorentzian - de Sitter Metric
1
2
2
2
2
2
2
2
ds = −dt + coshHt(dr +sin r(d +sin d ))
H 2
Thus one gets the idea that a wave function which varies exponentially with the three
metric h ij corresponds to an imaginary time Euclidean metric. On the other hand, a wave
function which oscillates rapidly corresponds to a real time Lorentzian metric.
Like in the case of the pair creation of black holes, one can describe the spontaneous
creation of an exponentially expanding universe. One joins the lower half of the Euclidean
four sphere to the upper half of the Lorentzian hyperboloid.
47